A Comparison of Bayesian and Frequentist Approaches to Analysis of Survival HIV Naïve Data for Treatment Outcome Prediction
Received Date: August 08, 2025 Accepted Date: August 26, 2025 Published Date: September 02, 2025
doi:10.17303/jaid.2025.12.103
Citation: Taisheng Li, Ling Chen, Jia Tang, Leidan Zhang, Liyuan Zheng, et al. (2025) The Risk of Weight Gain in Hiv Treatment-Naïve Individuals Antiretroviral Therapy Insti-Based and Non-Insti-Based Regimeds: A Retrospective Cohort Study. JHIV AIDS Infect Dis 12: 1-19
Abstract
Survival analysis is a statistical method for modelling the probability that a subset of a given population will survive past a certain time. In the context of HIV, this probability would represent the treatment failure. However, Frequentist methods dominated the survival analysis in the 20th century but the introduction of the Bayesian methods in the last decades it has been known to suffer from lack of use of probability statements in the interpretation of results.
In this study, we used dataset of HIV naïve patients to validate a Bayesian methods of survival analysis and compared the results to frequentist methods. Our analysis compares (i) calculation of probabilities of treatment failures of ARV combinations 1 and 2, (ii) tests for a difference in the survival experience of two combinations in the treatment of HIV, (iii) analysis of the Cox Model with Covariates.
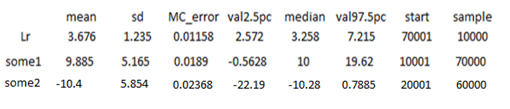
Across the data set, the Bayesian methods produced the probabilities of treatment failures for the first baseline ARV combinations as; 0.04124, 0.01034, 0.02973, 0.08952, 0.03765 and 0.03596 for combinations 1, 2, 3, 4, 5 and 6 respectively. While the likelihood ratio test of 3.676 and some 1 of 9.885 with credible interval of -0.5628 and 19.62 means HO of no significant difference between combinations was retained as the credible interval included zero. While the frequentist methods gave the log-rank value of 2.788 and P-value of 0.248 which means HO is retained. The Bayesian methods gave an overall HR of 0.8916 and Beta of -0.134 for combination 1 versus combination 2 means the risk of combination 1 is higher than that of combination 2. While the Frequentist method do not give an overall measure of risk.
The study, showed that Bayesian methods is a better option in survival analysis over traditional frequentist approach, although both methods yields similar results. However, the outlined Bayesian framework provides several benefits and uses data more efficiently. It is suitable for analysis of rare diseases and outbreak of pandemics as sample sizes are normally small, also a better option for analysis of HIV data as HIV data is hidden due to stigma. It provides a natural and principled way of combining prior information with data, within a solid decision theoretical framework.
Keywords: Antiretroviral therapy; log-rank; HIV naïve patients; likelihood ratio; Bayesian
Abbreviations
ARV: Antiretroviral; ART: Antiretroviral Therapy; CD4 count Differentiation; EFV: Efavirenz; FTC: Emtricitabine; HIV: Human Immunodeficiency Virus: HIV Drug Resistance; MAP: Maximum a Posterior; MCMC: Markov Chain Monte Carlo; TDF: Tenofovir; TDRMs: Transmitted Drug Resistance Mutation strains; RNA: Ribonucleic Acid.
Background
Survival analysis is a statistical method for modelling the probability that a subset of a given population will survive past a certain time. In the context of cancer, this probability would represent a recurrence of tumour, or remission (i.e. being disease-free) [1]. In the case of HIV, this is the probability of treatment failure and the effect of treatment outcome due to patients’ covariates which are of great importance [2]. The comparison between the two methods in terms of the coverage performance of the confidence and credible intervals, the frequentist methods exhibited strong under coverage, whereas the Bayesian credible interval performed as desired with a slight advantage over the Frequentist methods in terms of interval length [3-6].
On comparison the two methods on the results obtained in survival analysis, it was observed that the results were similar although the Bayesian methods had a slight advantage over the frequentist methods. There was no significant difference in survival predictions. However, the Bayesian methods provides more benefits when applied to parametric survival analyses, uses data more efficiently, is capable of considerably shortening the length of clinical trials, and provides a richer set of inferences [7,8].
On comparing the two methods, the Bayesian methods are a better option in survival analysis of rare diseases were the sample size is small. Also a Bayesian predictive probability can be designed to provide an analysis with any desired frequency including continuous assessment after each patient is observed [9-11].
Basic concept of Bayesian methods is given with results and then survival analysis is also carried out with the Frequentist approach using nonparametric methods and results compared for the first base line regimen of ARV drugs. The objective of this article was to critically review the use and reporting of Bayesian methods compared to frequentist approach in survival analysis.
Methods and Materials
Study Design and Study Site
The study was partitioned into two parts. The first part of the study involved the total number of newly diagnosed HIV individuals initiated with ARV drug during the year 2016. This dataset was used to calculate the probability of treatment failure of the first and second baseline regimens using the Beta-Binomial hierarchical model. The second part of the study was a retrospective study which was conducted from January 2016 to December 2016 involving one hundred, and seventy-four (174) randomly selected HIV-positive patients initiated with the antiretroviral therapy in Livingstone district health centres, Southern Province, Zambia. The study participants were selected from a pool of adult HIV patients who live in the Livingstone district. The extracted data from patients’ files consisted of two groups of 87 subjects in each combination. The method used for extraction of data included the covariates of each patient such as: regimen given, outcome of the treatment, gender, age CD4 count and weight were obtained every 12 weeks for 86 weeks. The dataset from these two groups was used to determine whether there was any difference in efficacy between the two combinations and the effects of covariates on individuals initiated with ARV drugs.
The survival probability was determined by the Kaplan Meier survival method for frequentist approach. Cox and Beta-Binomial for Bayesian methods were used to determine predictors of treatment failure.
Bayesian Approach
The Bayesian method begins with a sampling model for the observed data y= (y1.… ,yn) given a vector of unknown parameters ϑ. It shows this sampling model as a probability distribution f (y|ϑ). We view it as a function of ϑ and not of y; it is called the likelihood and written as L (ϑ: y). Note that L (ϑ: y) need not be 1 and may not be finite. Given any data value y, it is possible to find the value ϑ that maximizes the likelihood function, that is, ϑ =arg max L (ϑ: y) called the maximum likelihood estimate (MLE) for ϑ. In the Bayesian perspective, ϑ is an unknown random quantity. We call this a probability distribution for ϑ that summarizes any data y, called the prior distribution. Just like the likelihood has a parameter ϑ, the prior distribution has a parameter η called; hyper-parameter. Let us assume that the hyper-parameter η is known and write the prior as π (ϑ) ≡ π (ϑ |η). We then base inference about ϑ on the posterior distribution given by.
The Bayesian statistical approach was adopted in analysing the data. By using the fundamental properties of conditional probability, the posterior distribution in equation (1.1) was calculated using a Beta-Binomial hierarchical model.
Let the evidence Yi (i =1, 2,…, N) be independent and identically distributed from a binomial distribution, yi~bin (ni, ϑi). Suppose ϑi (i=1, 2, N) are parameters governing the data generating process is exchangeable from a standard population with Beta distribution, ϑi ~Beta (a, b) governed by hyper parameters, (a, b) ~ ϕ (a, b), the ϑi and ϕ (a, b) are random parameters where a and b are assumed known. Let p be a generic symbol for a density function. Consider a likelihood function p(yi| ϑi, ϕ ), a prior distribution p (ϑi |ϕ) and a hyper prior distribution p(ϕ) which produce the joint posterior distribution p(ϑi, ϕ| yi,. we use a Beta-Binomial hierarchical model to estimate the probability of treatment failure of the ARV drugs combination of the first- and second-line regimens. Hierarchical models are those with a hierarchical structure to the parameters and potentially to the covariates if the model is a regression model. The models are useful because they allow for the modelling of interactions between observed variables through the use of latent variables.
The Beta-Binomial hierarchical model provides the joint posterior distribution as
Which is proportional to the product of the likelihood function, the prior distribution and the hyper prior distribution, ignoring the constant denominator in equation (1.2). The use of the hyper prior distribution provides more information leading to opinions that are more accurate on the behaviour of a parameter.
Consider the probability of a patient switching from the first-line treatment with ϑi, as the probability of the virological failure for combination i is the quantity of interest in the analysis. The complement of this probability is the kernel probability of a patient remaining on the first-line regimen. We derive a joint probability model by combining the prior distribution Beta (a, b), the likelihood function p (y_i |ϑ_i,ϕ) and the hyper prior distribution p (ϕ). Thus from the full model,
From equation (1.3), we recognise that
Equation 1.4) is an interplay between the data y1 and the hyper parameters a and b in forming the posterior distribution where for each P (ϑi|yi,a,b)α ϑi a+yi-1 (1-ϑi)b+ni-yi-1. Thus the population of ϑi'S has ϑi||yi a,b~Beat(a+yi, b+ni-yi)where (a + y1) and (b + n1 + y1) are the posterior hyper parameters.
Bayesian Computation
The most common estimation algorithm in Bayesian methods is based on Markov Chains Monte Carlo (MCMC) sampling technique. MCMC is a unique method for estimating by simulation the expectation of a statistic in a complex model. Successive random selections form a Markov chain, and the stationary distribution is the target distribution of the simulations. Instead of solving the complicated integral in equation (1.1) analytically, the MCMC algorithm draws samples and computes expectations to produce a posterior distribution P (ϑ|y) of the quantities of interest. Several standard algorithms exist for carrying out MCMC, which converges to a target distribution such as, Metropolis (1953) & Hastings (1970), GIBBS Sampling, Gemman & Gemman (1984), Gelford and Smith (1990) and Casella & George (1984) produces a Markov Chain by selection from complete conditional distributions. The two standard algorithms are GIBBS Sampler (Gelford and Smith, 1990) and the Metropolis-Hastings (Hastings, 1970, Metropolis et al., 1953). When numerically estimating the normalisation constant, often the integral is of high dimension. Gelford and Smith (1990) showed that the joint estimates could be obtained by sequentially estimating each parameter while holding all others constant. The distribution of a parameter holding all other parameters constant is called full conditional distribution. When sampling from full conditional distribution, the parameters can be drawn directly. Otherwise, the parameters can be drawn indirectly using adaptive rejection sampling (Gilks and Wild, 1992) or the Metropolis-Hastings sampler methods [12].
A Markov Chain is formed by a sequence of random variables ϑ(0), ϑ(1), ϑ(2),…., ϑi+1~ p(ϑ|ϑi) the probability that a patient is on second baseline treatment given that they were in the first baseline treatment. This satisfies the Markov Chain properties of periodicity and irreducibility, but the process is not reversible. This is conditional on the value of ϑ (i), ϑ (i+1), is independent of ϑ (i-1)…ϑ(0).
Drawing samples from the link quantity of interest for ϑ , such as (ϑ1(1),…, ϑk(1)), (ϑ1(2),…, ϑk(2)),…, (ϑ1(N),…, ϑk(N)) ~p(ϑ|y), by drawing samples until the parameter convergence to a distribution called the marginal posterior p(ϑ1|y), which implies that
This is called Monte Carlo integration. Using the GIBBS sampling algorithm for MCMC sampling, the exact simulation can be obtained in the following manner:
Let a vector of unknown consists of k sub-components as ϑ= ϑ1,…..,ϑk, start with an arbitrary starting value, say (ϑ10, ϑ20,…., ϑk0) and t = 1,2,….,T perform the following steps:
The conditional distributions depend on complete conditions as parameters rely on these conditions ϑ (n) and provide a Markov Chain with a target distribution that expresses uncertainty ϑ. The sampler moves from the starting values to the posterior distribution and then fully explores that distribution. The draws are independent of the starting value when the first n iterations, known as the burn-in period, are discarded. The burn-in allows quick exploration of the posterior distribution. The subsequent draws estimate the posterior distribution and calculate the quantities of interest [13, 14]. Some theorems can be used to prove that chains converge to a limit as N→∞.
Theorem of Weak Laws of Large Numbers
If for y1, y2,…yn there are independent observations of the same random variables, all with mean µ, for every Ɛ ˃ 0, then p(|Mn-µ|≥ Ɛ) →0 as n→∞.
This theorem can be proved using Chebyshev’s Inequality or Characteristic functions.
The Theorem on weak laws of large numbers guarantees the convergence of chains to a stationary distribution as n→∞ even if the sample depends on the number of samples drawn. With fixed parameters of a and b in the beta prior distribution (equation 1.4) and r the number of success and n sample size increases E(\vartheta \mid r, n) \;\to\; \frac{r}{n} and the dispersion goes to zero. This means that as n increases, the posterior distribution becomes condensed, and sampling distribution takes over the prior distribution.
Results
The code given in Bugs code 1.1implements the Bayesian model, providing a full MCMC chain for each parameter. Chains produce estimates for the posterior distributions and other associated statistics, such as means, medians, standard deviations, and credible intervals. The results of the simulation with one chain are given in Table 1.1.
< Insert BUGS code 1.1 >
MCMC Convergence Diagnostics
The tool that can check for the convergence of parameters to a target distribution is called MCMC diagnostics. These tools check whether the sample generated accurately approximates the target distribution. MCMC diagnostics are used to check:
•Convergence: it is essential to know that the distribution of ϑ (t) goes closer to p (ϑ |y)?
•Effectiveness: how accurate do the distributions p (ϑ |y) are approximated from ϑ (t)?
The Probability distributions of treatment failure of first-line regimen on the ARV drugs combination
The characteristic of the Bayesian methods is that all conclusions are based on the joint posterior distribution, which addresses a range of questions with appropriate summaries of posterior distributions. In addition, it reports posterior sample parameters such as the mean, median and standard deviation, which are of interest either as a point estimate or credible interval within which the parameter lies with a probability of 0.95. The analysis was run 40,000 iterations, as shown in the "samples" column in the node statistics in Table 1.1 is the number of simulations, not the sample size of the data n = 174.
An MCMC chain was run with an adaption period of 10000 iterations with the start sample at 10001 to 40000 for each of the six nodes. Table 1.1 presents summary statistics on data for the first-line regimen on ARV drug combinations. The statistics such as; the mean, standard deviation (sd), Monte Carlo standard error (MC error) of the posterior sample mean, the point estimate of 2.5 % percentile, median and the point estimate 97.5% percentile are reported in Table 1.1.
The calculated values in Table 1.1 show that MC error < 1 − 5% of posterior sd as the rule of thumb in Bayesian data analysis has been satisfied. Generally, a mean or median of the posterior samples for each parameter of interest as a point estimate of 2.5% and 97.5% percentiles of the posterior samples for each parameter gives a 95% credible posterior interval. The interval within which the parameter lies with a probability of 0.95. The results in Table 1.1 indicate that the posterior distribution of p, the rate of treatment failure due to TDRMs, is approximately normal with μ = 0.04124 and σ = 0.01779 for theta (1). These numbers are computationally accurate to about ±8.874E-5 (MC error). Consequently, mean μ = 0.041 and σ = 0.018 with median of 0.03873 and a credible interval of [0.014, 0.083] which does not contain zero are reported. The rest of the treatment probabilities for combinations 2, 3, 4, 5, 6 are reported in Table 1.1 as 0.01034, 0.02973, 0.08952, 0.03765 and 0.03596 respectively are given with their respective Mc errors and 95% credible intervals. From the results it is easy to identify a combination with lower probability of treatment failure which could be the optimal combination to be prescribed for a patient in the presence of transmitted drug resistance mutation test results [2].
The heading in Table 1.1 means in column 1 is the parameter of each combination for example, theta 1 is combination 1, showing the mean probability failure of 0.04124, with standard deviation of 001779, with MC error which is the degree of accuracy of results as 8.87E-05, with credible interval of [0.014, 0.08279], median of 0.387, sampled from 10001 to 40000. This interpretation applies to all combinations that is theta 2 up to theta 6.
Bayesian Analysis Tests for a Difference in the Survival Experience of Two Combinations in the Treatment of HIV
The likelihood test compares the overall survival experience of two or more groups by comparing the first-ordered observation to the last-ordered observation (of time to event). Bayesian procedures mimic the conventional methods, although the interpretation of the test is a strictly Bayesian approach. The likelihood test compares the two groups by comparing the observed minus the expected number of events (event, survival, and so on), which are normalised by the variance of the difference.
The expected number of failures for combination 1 was computed as follows:
It is assumed that the failure probability (and the probability of a censored observation) then the two combinations are the same at each period. Note that the number of failures and the number of censored observations for each period follows a binomial random variable; hence, the number at risk also is a random variable. Observe that the number at risk at any time decreases by the number of failures and the number of censored observed.
The Bugs code.1.2 calculates the difference in the observed minus expected events for combination 1, assuming no difference in the probability of failure between the two. The observed minus expected differences for combination 2 differ only in sign to those of combination 1. Observations of treatment failure or censored events are assumed to have a binomial distribution, whose corresponding probabilities are given Beta (.01, .01) prior distributions. This induces a posterior distribution to the number of expected events given by (equation 1.6), and this induces a posterior distribution to the observed minus expected differences of combination 1. The interest is to tests for a difference in the overall failure between the two combinations, which is given as:
Where m = 32 is the number of observed times for each combination. Also, the sum of the observed minus expected differences for Combination 2 is given as:
\text { some } 2=\sum_{i=1}^{i-m}\left(d_{2 i}-a_{2 i}\right)\:\:\:\ 1.8Wherea_{2 i}=\left[\frac{R 2(i)}{(R 1(I)+R 2(i)}\right]\left(d_{1 i}+d_{2 i}\right) \:\:\:\: 1.9
This is the expected number of failures for combination 2 for the ith time. The Bayesian method was used to test for the difference in failure time between combinations. On comparing the two combinations, which are ordered in time, a likelihood test was adopted. Although its interpretation of results is strictly Bayesian, the likelihood test, which mimics the conventional methods of log-rank test, was used. The likelihood test compares the overall of the two combinations of the observed minus the expected number of events, which are normalized by the variance of the difference. For example, if there is no difference in failure rate between combinations, then it would be expected that half would be positive, and the other half would be negative, and the average would be zero. Alternatively, if the 95% credible interval includes zero, it is concluded that there is no significant difference in failure rate between combinations.
< Insert BUGS code 1.2 >
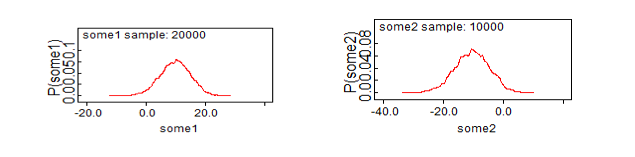
The Bayesian methods depend on some 1 on the interpretation of parameters (equation 1.7), that is the sum of the differences of the observed failures minus the expected (with the assumption that the overall failure pattern is the same for the two combinations), the number of failures for ordered values of failures and censored times for combination 2. The posterior distribution is given in Table 1.2 with a posterior mean of 9.885 with an sd of 2.165, a 95% credible interval of (-0.5628, 19.62), and a median of 10. It can be observed that the credible interval includes zero, means there is no difference in efficacy between combinations. Similarly, the values for some 2 (equation 1.8), which is the sum of the observed minus expected failure rate for combination 2 was investigated for the differences in the failure rate of the two combined using the density plots Figure 1.3,
Furthermore, the parameters that measures the overall difference in failure rate are the likelihood ratio (Lr), the posterior distributions of some1 (4.4.6) and the posterior distribution of some 2 (4.4.7. In this analysis, the Lr has a posterior mean of 3.676, a median of 3.258 and a 95% credible interval of (2.572, 7.215) Table 1.2), imply that there is evidence that the two combinations do not differ in failure rates.
The posterior densities of some 1 and some 2 are shown in Figure 1.3. If there is no difference in the overall failure pattern between the two combinations, some1 and some 2 would be expected to tend to 0 on average Figure 1.3 shows that both combinations tend to zero on average, implying no difference in failure rates between combinations.
For the Bayesian, the likelihood ratio parameter is
L_r = \frac{\text{some1} \cdot \text{some1}}{e_1} \;+\; \frac{\text{some2} \cdot \text{some2}}{e_2}
Where some are given by equation 1.7 and some 2 is given by
e_1 = \sum_{i=1}^{32} a_{1i}
Is the total number of expected failure for combination 1, and?
e_2 = \sum_{i=1}^{32} a_{2i}
Is the total number of expected failure for combination 2?
The Bayesian methods depend on some 1 parameters (1.7), the sum of the difference between the observed numbers of failures minus the expected (with the assumption that the overall failure pattern is the same for the two combinations) number of failures for ordered values of failures and censored times for combination 2. The posterior distribution is given in Table 1.2 with a posterior mean of 9.885 with an sd of 2.165, a 95% credible interval of (-0.5628, 19.62), and a median of 10. It can be observed that the credible interval includes zero. This indicates that there is no difference in treatment failure between combinations.
This Lr of 3.676 is the likelihood ratio of combination 1 and 2, with has a credible interval of 2.572 to 7.215 (Table 1.2) is similar to the log-rank (mantel cox) of 2.788 in Table 2.1 from the conventional methods since it is included in the credible interval of the Bayesian approach of hypothesis testing of the null hypothesis. This shows that there is evidence to conclude that at a 5% level of significance, there is no difference in failure rates between combination 1 and combination 2 for both methods.
A conventional procedure based on the Chi-square statistic of 2.788 under the null hypothesis indicated no difference in failure rates of the two combinations. While the likelihood ratio value of 3.676 from the Bayesian method gave some 1 credible intervals of -0.5628 to 19.62 includes zero means the null hypothesis was retained. The credible interval of some 1 includes the Chi square statistic of 2.788 means both methods retained the null hypothesis of no difference in efficacy between combinations.
Cox Model with Covariates
In assessing the effect of ARV combinations on time to events, all available characteristics of a patient must be included in the analysis. That means variables such as age, gender, regimen, CD4 counts, weight, and gender must be included in the model. Estimating the ARV combinations ' survival probabilities can determine the variables that affect treatment failure time. When the CD4 counts is included, it is expected that the hazard ratio of the combined effect to be modified, and the estimated survival probabilities will also change. The following code statements are included in the bug’s code.
Id[i, j] <- Y [i, j]*exp(beta[1] * x1[i]+beta[2]*x2[i]) * dL0[j] includes the covariate (log CD4 counts) in the model, and the code is as follows:
comb.1[j] <- pow (exp (-sum (dL0[1: j])), exp (beta [1] * 1+beta [2] *2.33));
Comb.2[j] <- pow (exp (-sum (dL0[1: j])), exp (beta [1] * 2+beta [2] *3.21));
That means both the regimen indicator and the log CD4 counts are included in computing the posterior distribution of the survival proportions for both combinations. The regimen indicator is 1 for combination 1 and is for combination 2, while the coefficient beta is the effect of the combination on the failure times, and beta [2] is the effect of the log of the CD4 counts on the failure time. The average CD4 counts for combination 1 was 2.33, while the average CD4 counts for combination 2 was 2.21.
< Insert BUGS code 1.3 >
The results provided in Table 1.3 gives values of the parameters for the analysis. The HR for beta [1], the difference in the two combinations, is estimated as 0.8651 with a posterior median of 0.8525 and a 95% credible interval of (0.6246, 1.177). HR for beta [2], which measures the effect of CD 4 covariates, has the posterior mean of 0.7429 with sd of 0.2176, the median of 0.7093, and a 95% credible interval of (0.4289, 1.251). HR for beta [3] the effect of gender has the posterior mean of 0.7165 with sd of 0.1308, the median of 0.7058, and a 95% credible interval of (0.4923, .09963). HR for beta [4] the effect of weight has a posterior mean of 0.9975 with sd of 0.009264, the median of 0.9978, and a 95% credible interval of (0.9802, 1.017). HR for beta [5] the effects of age have a posterior mean of 1.003 with an sd of 0.01047, a median of 1.004, and a 95% credible interval of (0.9842, 1.025).
Table 1.3 provides beta coefficients of the covariates regimen, log CD4 counts, gender, weight and age. The values are: beta [1] = -0.1562, beta [2] = -0.3103, beta [3] = -0.3512, beta [4] = -0.00404 and beta [5] =0.0045. Beta [4] is the weight of the patient and beta [5]. The age of patients has no impact on time to failure. However, the other covariates have an impact on time to failure. For example, the hazard ratio of beta [1], which is the regimen, has a hazard ratio of 0.8651, with a median of 0.8525 and a 95% credible interval of (0.6246, 1,177). The negative beta value means a lower risk for combination 1 in the sample. The estimated risk of failure due to combination 1 is exp (-0.1562) = 0.8554. That is, combination 1 has 0.8554 the risk that combination 2 has a failure, or combination 1 has a 14.46% lower risk of failure than combination 2. The estimated risk of 0.8556 indicates that combination 1 has a 14.46% lower risk of failure than combination 2. Accounting for sampling variability, the decrease in risk for combination 1 could be 37.54% or as small as zero.
The Conventional Approach to Survival Analysis of HIV Naïve Patients
Survival analysis is normally carried out with the help of nonparametric methods, semi - parametric and parametric methods [15].
Non-Parametric Methods
Kaplan-Meier Estimator is a non-parametric method that is used to estimate the overall likelihood of survival from the given set of survival data. The Kaplan Meier method does not assume any distribution for the survival time observed in the study [16].
A conventional approach was adopted on survival analysis relates to the time for the HIV naïve patient to experience the treatment/virological failure of the first baseline regimen. The standard methods of survival analysis construct a Kaplan Meier curve which estimates the survival rates of HIV patients who experience treatment failure of HIV patients. The cox model was also used to search for the association between the HIV patients' survival time and risk using the cox models. This model estimates the treatment effect after accommodating other characteristics and assessing the risks of treatment failure for HIV patients, given their predicted characteristics.
The Kaplan Meier Curve
The Kaplan Meier curve shows the survival chances (the total chances of not experiencing treatment failure at a given time for baseline combinations). Thus, the chances of a patient being alive are the cumulative consequences of a patient's circumstances up to time ti. The chances of a patient being alive for up to a week ti calculation is given by:
\frac{n_i-d_i}{n_i}=\frac{\text { No.not experienceventheweekbefore-No.experiencingevent onweekt }}{\text { No.notexp erienceventheweekbefore }}Survival\: until \:week \:$t_i: S(t_i) = \frac{n_i - d_i}{n_i} \cdot S(t_{i-1})\:\:\:\:\:2.1
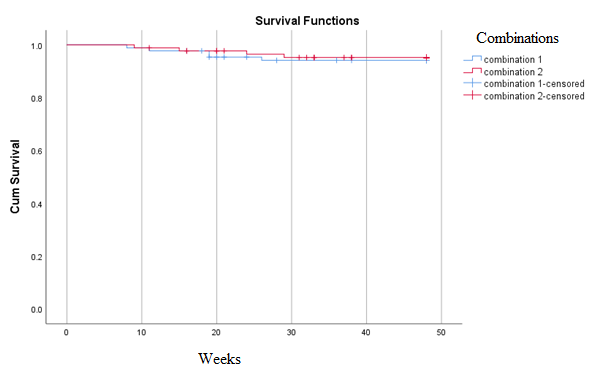
Figure 2.1 displays a Kaplan Meier plot that show the survival probability for Combination 2 (TDF+FTC+EFV) that is superior to the other combinations around 30 weeks as the survival probability is larger than all combination, but they generally look the same.
The Kaplan Meier Survival curves obtained from the analysis is shown in Figure 1. The survival curves indicate that the CABG patients have greater survival times than the PCI patients.
It can be concluded that the ARV combinations used in Zambia are not significantly different in suppressing the viral load as indicated in the Kaplan Meier curve as indicated in Figure 2.1 In survival analysis, the survival probabilities are usually reported at a particular time point on the curve, and the median survival time (the time for which 50% had the event) is registered. Thus, for example, the overall median estimated survival time between ARV and treatment failure initiation is 40, 42 and 39 weeks for combinations 1, 2 and 5, respectively as shown in Figure 2.1
The Test for Log Rank
The Log-rank tests the null hypothesis of no difference in survival times between the combinations of ARV at any time points up to 48 weeks. The test compares the data and theoretical results for ARV combinations. It was assumed that the trial of the survival times was continuous and that the ratio of outcome risks occurring in combination 1 contrasted to the risk in combination 2 remains constant (proportional hazard assumption).
The test statistic for comparing two combinations, A and B:
The expected values can be calculated as:
Where di = total events at the time ti,nAi = total patients in danger at a time ti in cohort A and = total patients at risk. SPSS was used for computations and obtained the following results:
The log rank test results given in the Table 2 shows that the survival times CABG Patients is Significantly greater than the PCI patients’ survival time (p<0.05).
The overall comparison from a frequentist perspectives give a Log rank of 2.788 with 2 degrees of freedom and a p-value of 0.248 means there is no significant difference in efficacy between combinations 1 and 2.
The equality of survival distributions was tested for the different levels of first-line. The regimen was found from the survival distribution. The test statistics were compared in Table 2.1 value of the Chi-square distribution at 5% significance level, 2 df, and the critical value was .The test statistic was 2.788 from Table 2.1; this value is less than the critical value Hence, the null hypothesis is accepted and concludes that there is no evidence of a difference in survival time between combinations 1 and 2. The p-value from Table 2.1 is 0.248 and is greater than the significant level of 0.05, meaning that the null hypothesis of no difference between combinations is accepted. Therefore, there is enough evidence for the risk difference between the combinations 1 and 2. The other tests are shown in Table 2.1, such as Breslow (Generalized Wilcoxon), which measures the middle of the period, and Tarone-ware measures the beginning of the period. Both show no evidence of a difference between combinations 1 and 2 [17].
Regression Analysis of the Cox Model
Regression analysis of the cox model contrasts the risks (as a ratio) of combinations in which many characteristics are considered. The risk of an event is the probability of time to an event at the endpoint (in this case, treatment failure) at a time point, given that the patient had no event up to that point .
The model for the regression analysis of many variables is given by:
The hazard function for modelling is the form \lambda_i(t) = \lambda_0(t) \exp(\beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_k x_{ik}), where λi (t) = risk ratio ti for the individual, λ0 (t)= initial hazard function.
To check for significant effects of the covariates in the significant column in Table 2.2 gives the probability values. The probability values are compared with a 5% level of significance using the standard table values. To interpret the covariates' effects, use the exponential (beta) column in Table 2.2. This column represents the risk ratio which explains the predicted change in the risk for any unit growth of the predictor. Cox's regression model has one assumption to be satisfied: that is, the comparable risk ratio among combinations at any time is constant. Table 2.2 shows that gender for a patient with a probability value of 0.180 shows no observed risk of treatment failure for HIV infections over sex. There are no effects on the predictors such as age, gender, and drug combination being used; they all show no significant difference at the 5% level. The p-values are: 0.66, 0.180, 0.124, 0.804 and 0.097 respectively. However, the probability value of CD4 counts, which is the CD4 counts at diagnosis, has a probability value of 0.048, which shows a significant difference at 5%, and the weight of a patient at diagnosis has a probability value of 0.011, which is also significant at 5%.
For definitive data, the risk ratio can be interpreted from Table 2.2 directly on variables in the equation column of exp (β). The risk ratio contrasts the risk of outcomes occurring between two variables. For example, if the hazard ratio is greater than 1, the risk of the event occurring in combination 1 is higher than that of combination 2.
The formula used for the calculating the hazard ratio is:
The results of the CD4 counts indicated the effectiveness in monitoring the disease's progression. That means for any unit added to CD4 counts; the risk reduces by. For example, for any five units added to the CD4 counts, the risk reduces by a 49.9% decrease. On inspecting the regression coefficient in Table 2.2, the values for the variables age, CD4 counts, and drug1 (2) are negative, while weight has a 0 coefficient, which predicts HIV 1 patients with the more significant values of variables as indicated in Table 2.2 [26].
Conclusion
The Kaplan Meier curves and log rank test shows no significant difference in performance between combinations 1 and 2.
Discussion
Bayesian approach to Survival analysis can be used to carry out the survival analysis due to its ability to handle design and analysis issues in survival model. The main reason for the use of Bayesian approach is due to its flexibility and operating characteristics. [8, 18]. The difference between the Bayesian and the frequentist methods is in terms of uncertainty about unknown parameters in a model which is expressed through a distribution, called the prior distribution [11].
The main inferential tool in the Bayesian method is called the posterior distribution [19], which is constructed from the data, and the prior distribution. The proper choice of priors plays an important role in the success of the Bayesian survival analysis in achieving its objectives [19].
In this analysis we carried out a comparison study of Bayesian versus frequentist methods of survival analysis of HIV naïve patients initiated with ART [20]. We calculated the probability of HIV treatment failure of ARV using a Beta-Binomial model [2]. The results obtained in Table 1.1 were unique as they were obtained from the Bayesian methods only as the frequentist methods do not make probability statements about the parameter of interest.
Interpretation of Probability
Frequentist approach does not make direct statements about parameters whereas Bayesian approach makes direct statements about parameters. Table 1.1 give the probabilities of treatment failures of each combinations such as: 0.04124, 0.01034, 0.02973, 0.08952, 0.03765 and 0.03596 for combinations 1, 2, 3, 4, 5, and 6 respectively. Based on these probabilities a Physician can make informed decision on the optimal choice of combination for a patient in relation to the Transmitted drug resistance mutation strains test [2, 21]. Null Hypothesis HO:
There is no significant difference in treatment failure between combinations 1 and 2 at or 5% level of significance.
A.Frequentist Approach
When the treatments are repeated under the same condition with new data each time, only in 5% of the times the null hypothesis will be rejected wrongly (when it is actually true). Table 2.1 give a Log- Rank value of 2.788 with a p- value of 0.248, means there is no significance difference in efficacy between combinations 1 and 2 at 5% level of significance.
B.Bayesian Approach
Bayesian approach will give exact probability of null hypothesis being true which is straight and easily interpretable. In the above case, the probability of null hypothesis being true is only 5%. Table 1.2 give a Likelihood ratio statistic of 3.676, and the credible interval for some 1 as -0.5628 and 19.62 means the null hypothesis is retained since the credible interval includes zero. It can be observed that the credible interval for likelihood ratio test of [2.572, 7.215] includes the Log-rank statistic of 2.788, means the two methods are in agreement in testing the null hypothesis.
In frequentist approach, the traditional confidence interval is interpreted as if we construct confidence intervals over time from the samples drawn from the population, which means the 95% of confidence intervals constructed will contain the parameter of interest. It will not specify the probability that the parameter lies in the interval, that is, there is a 95% chance that the survival time lies in the interval (Akbari et al., 2019). However, the Bayesian approach, gives the credible interval or the Bayesian highest posterior density interval gives us the 95% probability that the unknown parameter mean survival time lies in the interval [18].
On comparing the parameter values it can be observed that the beta values from Bayesian method are similar to beta values for Frequentist method [1, 4]. The beta value for regimen is -0.156 for Bayesian method and -0.283 for Frequentist method with HR beta of 0.865 and Exp.beta of 0.754 respectively. The confidence interval of [0.540, 1.052] for Frequentist and credible interval of [0.6246, 1.177] for Bayesian method. However, the Bayesian method provides a value of MC error of 0.005481 to indicate the degree of accuracy of parameters which is not found in Frequentist methods. The rest of the parameters can be compared from Table 1.3 for Bayesian approach and Table 2.2 for Frequentist approach.
The Kaplan Meier Curve analysis is a Frequentist approach only (Figure 2.1) and not Bayesian.
A powerful feature of the Bayesian approach is that all inferences are based on the joint posterior distribution. This implies that the approach can address wide range of substantive questions by appropriate summaries of the posterior distribution. It typically reports:
• Either mean or median of the posterior samples for each parameter of interest as a point estimate,
• 2.5% and 97.5% percentiles of the posterior samples for each parameter to give a 95% posterior credible interval (interval within which the parameter lies with probability 0.95).
Conclusion
The paper provides a comparison overview of frequentist and Bayesian approaches to survival analysis with the help of HIV treatment naïve dataset using WinBUGS software. The results obtained in both methods were similar. However, the outlined Bayesian framework provides several benefits as it uses data more efficiently and it provides a natural and principled way of combining prior information with data and has the ability to update results as new evidence is available. Also, the Bayesian approach is suitable for survival analysis of HIV data which is invisible due to stigma. The results obtained may help provide a feasible, reliable, and valid methods to assess the future management interventions of HIV in improving patients’ outcomes.
Limitations of the Study
In this study, secondary data was used in building models hence authenticity and accuracy of the data used cannot be guaranteed. The results may change depending on the accuracy of the data.
Appendix Information
https://www.jscholaronline.org/articles/JAID/Appendix-Information.pdf
Acknowledgements
The authors wish to thank the University of Zambia and the University of South Africa for sponsoring the work. We are grateful to the Zambia National Health Research Authority for providing access to the data and permission to publish the results. We greatly appreciate the constructive comments from the reviewers.
Authors’ contribution
This work was done in collaboration between authors. UNH conceptualized the study and conducted data analysis. PMN provided guidance in the analysis, conducted literature review and compiled entire manuscript. All authors read and approved the final manuscript.
Funding
University of Zambia contributed in employing UNH while University of South Africa contributed in employing PMN. No direct funds were obtained for this work.
Availability of Data and Material
The data can be made available, on request from the corresponding author.
Ethics Approval and Concept to Participate
The permission to use data was obtained from the Zambia National Health Research Authority.
Consent for Publication
Not applicable
Competing Interests
The authors declare that they have no conflicting interests.
- Abi. R, Fagbamigbe A, Akinwande A (2020). Comparison of Bayesian and Frequentist Survival Analysis Methods in Modelling of Prostate Cancer Survivorship in Oyo State, Nigeria.
- Haankuku U, Njuho P (2021). The Estimation of Transmitted Drug Resistance Mutation Strains Probability in the Treatment of HIV Using the Beta-Binomial Model - PubMed [WWW Document].
- Flor M, Weiß M, Selhorst T, Müller-Graf C, Greiner M (2020). Comparison of Bayesian and frequentist methods for prevalence estimation under misclassification. BMC Public Health 20, 1135.
- King GB, Lovell AE, Neufcourt L, Nunes FM, (2019). Direct Comparison between Bayesian and Frequentist Uncertainty Quantification for Nuclear Reactions. Physical Review Letters 122, 232502.
- Svenja E, Seide, Katrin Jrnsem, Meinhard Kieser (2020). A comparison of Bayesian and frequentist methods in random‐effects network meta‐analysis of binary data - Seide - 2020 - Research Synthesis Methods - Wiley Online Library [WWW Document].
- Westland JC, (2022). A comparative study of frequentist vs Bayesian A/B testing in the detection of E-commerce fraud. Journal of Electronic Business & Digital Economics 1, 3–23.
- Abidoye Akinwande, (2020). (PDF) Comparison of Bayesian and Frequentist Survival Analysis Methods in Modelling of Prostate Cancer Survivorship in Oyo State, Nigeria [WWW Document].
- Bartoš F, Aust F, Haaf JM, (2022). Informed Bayesian survival analysis. BMC Med Res Methodol 22, 238.
- Juhan, N., Zubairi, Y.Z., Mohd Khalid, Z., Mahmood Zuhdi, A.S., 2020. A Comparison Between Bayesian and Frequentist Approach in the Analysis of Risk Factors for Female Cardiovascular Disease Patients in Malaysia. ASMSJ 1–7.
- Kaizer A, Zabor E, Nie L, Hobbs B, (2022). Bayesian and frequentist approaches to sequential monitoring for futility in oncology basket trials: A comparison of Simon’s two-stage design and Bayesian predictive probability monitoring with information sharing across baskets. PLOS ONE 17, e0272367.
- Taheri Soodejani M, Tabatabaei SM, Mahmoudimanesh M, (2021). Bayesian statistics versus classical statistics in survival analysis: an applicable example. Am J Cardiovasc Dis 11, 484–8.
- Robert CP, (2015). The Metropolis–Hastings Algorithm, in: Wiley StatsRef: Statistics Reference Online. American Cancer Society, pp. 1–15
- An L, Brooks S, Gelman A, (1998). Stephen Brooks and Andrew Gelman. Journal of Computational and Graphical Statistics 7, 434–55.
- Bernardo JM, (1979a). Reference Posterior Distributions for Bayesian Inference. Journal of the Royal Statistical Society: Series B (Methodological) 41, 113–28.
- Stel VS, Dekker FW, Tripepi G, Zoccali C, Jager KJ, (2011). Survival Analysis I: The Kaplan-Meier Method. NEC 119, c83–8.
- Sedgwick P, Joekes K, (2013). Kaplan-Meier survival curves: interpretation and communication of risk. BMJ 347, f7118.
- Wellek S, (1993). A Log-Rank Test for Equivalence of Two Survivor Functions. Biometrics 49, 877–81.
- Brard C, Le Teuff G, Le Deley M-C, Hampson LV, (2017). Bayesian survival analysis in clinical trials: What methods are used in practice? Clin Trials 14, 78–87.
- Bernardo JM, (1979b). Reference Posterior Distributions for Bayesian Inference. Journal of the Royal Statistical Society: Series B (Methodological) 41, 113–8.
- Abi R, Fagbamigbe A, Akinwande A, (2020). Comparison of Bayesian and Frequentist Survival Analysis Methods in Modelling Of Prostate Cancer Survivorship in Oyo State, Nigeria
- Kantzanou, et al, (2021). Transmitted drug resistance among HIV-1 drug-naïve patients in Greece - ScienceDirect [WWW Document].
- Akbari M, Fararouei M, Haghdoost AA, Gouya MM, Kazerooni PA, (2019). Survival and associated factors among people living with HIV/AIDS: A 30-year national survey in Iran. Journal of Research in Medical Sciences 24, 5.
- Bende R, Thomas A, blettner M, (2005). Generating survival times to simulate Cox proportional hazards models - Bender - 2005 - Statistics in Medicine - Wiley Online Library [WWW Document].
- Hong H, Carlin BP, Shamliyan TA, Wyman, JF, Ramakrishnan R, Sainfort F, Kane RL, (2013). Comparing Bayesian and Frequentist Approaches for Multiple Outcome Mixed Treatment Comparisons. Med Decis Making 33, 702–14.
- Myers, et al, (2012). Transmitted Drug Resistance Among Antiretroviral-Naive Patients with Established HIV Type 1 Infection in Santo Domingo, Dominican Republic and Review of the Latin American and Caribbean Literature | AIDS Research and Human Retroviruses [WWW Document].
- Ngwa JS, Cabral HJ, Cheng DM, Pencina MJ, Gagnon DR, LaValleyMP, Cupples LA, (2016). A comparison of time dependent Cox regression, pooled logistic regression and cross sectional pooling with simulations and an application to the Framingham Heart Study. BMC Medical Research Methodology 16, 148.



Tables at a glance
Figures at a glance