Full Text Article

Introduction

Conventionally, the product quality specification and control chart limits are determined as the mean plus and minus 3 standard deviations with the assumption that the quality data is normally distributed. These limits are corresponding to the interval centered at mean with coverage of 97.3% of the distribution. Practically, it is determined by sample mean plus and minus 3 sample standard deviations. Such an interval is not a confidence interval of the statistical interval that covers 97.3% of the population. Statistically, we need to take consideration of the estimation error of such an interval. The statistical intervals that covers a fixed proportion of the population with a given confidence level is called tolerance interval. It has been proposed to use a two one-sided tolerance intervals approach for a drug product quality specification determination [3,4]. In order to avoid overestimating the tolerance interval when the coverage p is large, [1] proposed a precision criterion for the sample size requirement for the estimation of two one-sided tolerance intervals with 80% to 99% coverage as the quality specification. For a given confidence level, 1- α (e.g. 95%) and coverage percentage p, the tolerance interval may lead to coverage much larger than p when the sample size is small [5]. In order to derive a precise tolerance interval, [6] proposed a “goodness” criterion for sample size determination.

However, often time the continuous quality data may be distributed with a skewed unknown distribution, a multimodal distribution or a truncated normal distribution. In this report, we adapt Wilks’ proposal of using order statistics to determine the limit of the one-sided tolerance interval [2]. Based on Wilks’ method, we can determine the minimum sample size requirements for one-sided and two onesided tolerance intervals with a targeted order statistic as the limit(s). The limits determined with Wilks’ method often leads to a tolerance interval with coverage less than P when the sample size is small and larger than P when the sample size is large. In the literature, to overcome such weakness, method of interpolation of order statistics was proposed to improve the precision. In this paper, we discuss the application of Wilks’ method and some improvement methods based on the interpolation of order statistics for the determination of product quality specification. We also propose an extension of the improved method to the tolerance interval estimation for sample sizes that are not derived directly using Wilk’s method.

This paper is organized as follows. We state [2] approach and its extension to one-sided and two one-sided tolerance intervals in Section II. The sample size determination method and tables of minimum sample size requirement are presented in Section III. The method of using interpolation of order statistics to improve the precision will be discussed in Section IV. For sample size not listed in the tables, we propose an interpolation extension from the tables. It will also be presented in Section IV. A simulation study is conducted to demonstrate the improvement of interpolation methods to the Wilks’ (1941) approach. The summary and conclusion will be given in Section V.

WILKS (1941) APPROACH (From Chapter 8 of Statistical Tolerance Regions: Theory and Application by K. Krishmoorthy and Thomas Mathew)

Let X₁ , X₂ ,…,X_n be a sample from a population with a continuous distribution F_X (x). Let X(i) denote the ith smallest of X₁ ,X₂ ,…,X_n . Then

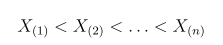
are the order statistics for the sample. Let Y=F_X (X).

Then Y~Uniform (0, 1). Consider the empirical distribution

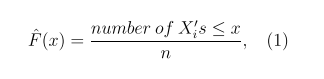
the number of observations 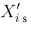≤ a given value x is n 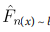binomial (n, F_x (x)). The probability density function (pdf) of X(i) is

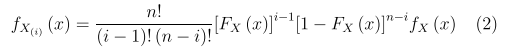
where f_X(x) is the pdf of X.

In order to construct a nonparametric (p, 1-α) lower tolerance interval limit, we need to find the positive integer k so that

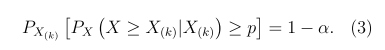
The probability on the left hand side of (3) can be expressed as

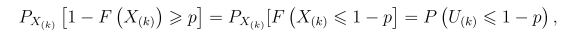
with

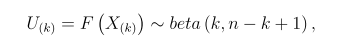
where beta (a, b) is beta distribution with parame- ters a and b. [7] has shown that

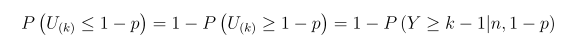
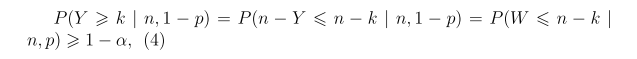
where y ~ binomial (n, 1-p), and W = n-Y ~ binomial (n,p). Thus, X_(k) is the desired (p,1-α) lower tolerance limit if k is the largest integer that satisfies (4). To construct a (p,1-α) upper tolerance limit, we need to find the largest positive integer m to satisfy

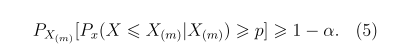
If we construct the lower limit X_(k) and upper limit X_(m) of one-sided tolerance intervals derived from (p,1-α/2), the two one-sided tolerance intervals is then defined as (X_(k),X_(m)). With the same n, p and α, it is easy to see that m = n-k+1.

Sample Size Determination for Estimation of OneSided and Two One-Sided Tolerance Intervals

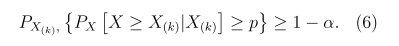
For any fixed sample size n, there may not exist order statistics that satisfy the requirements of one-sided tolerance limit. Let us consider sample size n requirement for estimation of (p,1-α) two-sided tolerance intervals in the form of (X_(k),X_(n)), for any given k. That is, to solve for the smallest n for the following equation,

It can be simplified to

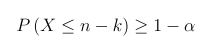
where X ~ Binomial (n,p). It is held if and only if

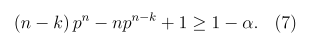
The sample size requirement for the two one-sided tolerance interval, (X_(k),X_(n-k+1)), can be determined based on the formula above. For α=0.05 and a given value of k and p, the sample size is the minimum N such that

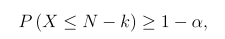
where X ~ Binomial (n, (1+p/2). The (p,1-α) two one-sided non-parametric tolerance interval, (X_(k)X_(n-k+1)), has the following property

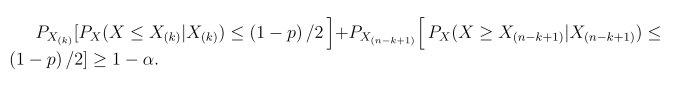
We calculate the sample size requirement for (X_(k)X_(n-k+1)) to be the two one-sided tolerance interval (p, 0.95) for p=0.8, 0.9, 0.95 and 0.99. The results are given in Table 1.

For one-side tolerance interval (p, 0.95) for p=0.8, 0.9, 0.95 and 0.99 can also be calculated with formula (7). The results are given in Table 2.

Similarly, we calculate the coverage p for a given tolerance interval (X_(k),X_(n-k+1)) for a given k and n. The true coverage p (with 95% confidence level) for selected k and n are given in Table 3.

Modified Wilks’ (1941) Approach

As shown in Section III, for tolerance interval (p,1-α) and any n satisfies sample size requirement, X_(K) is the lower limit of confidence interval of (p,1-α) if k is the largest integer satisfying the inequality [4]. Therefore, the confidence interval (X_(k),X_(n)) would have a confidence level and (X_(k-1), X_(n)) would be a tolerance interval with confidence level 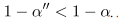A naïve modification would be use the average of X_(k) and X_(k+1) to replace X_(k) as the lower limit. It is represented as L_(X),

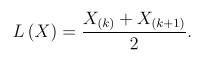
[8-10] investigated interpolation of two order statistics to improve the precision of the estimate. The interpolation can be expressed as follow,

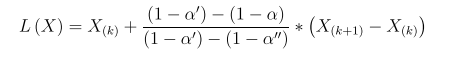
[11] presented a detailed discussion of the interpolation methods and proposed an extrapolation for tolerance interval limit based on sample sizes smaller than the minimum required. However, for quality specification, the coverage is typically high and often the range of values are restricted, we don’t recommend to use the extrapolation method for quality specification.

We also propose a method to determine the lower limit for any given sample size n between S_(k), the sample size required for the kth order statistics, and S_(k+1), sample size required for the (k + 1)th order statistics.

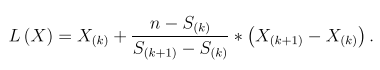
For example, with sample size = 150, for a tolerance interval of 95% coverage and with 95% confidence level, the lower limit of the two one-sided tolerance interval should be

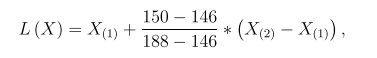
where X₍₁₎ and X₍₂₎ are the smallest and the second smallest observations respectively.

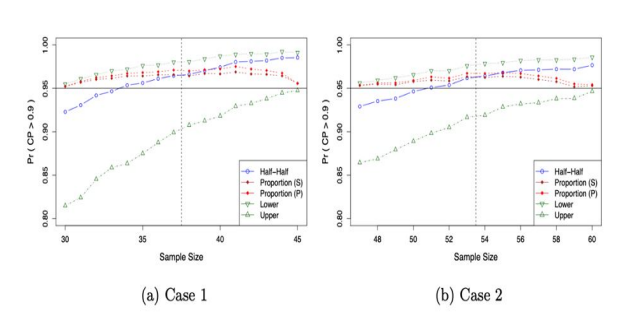
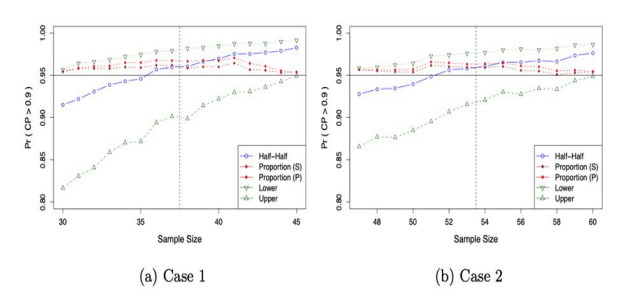
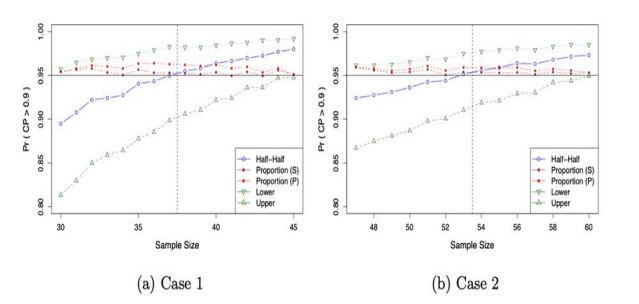
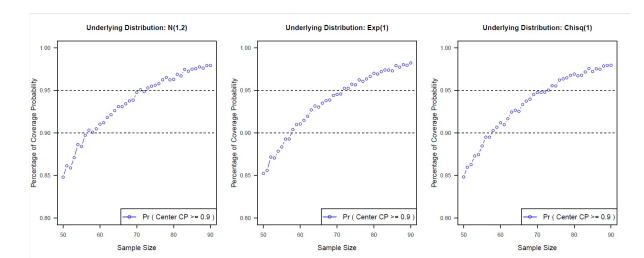
In order to illustrate the improvement of the confidence level of modified Wilks’ approach. We compare the three modified approaches or tolerance interval (0.90, 0.95) with Wilks’ approach and use the X_(k+1) as the lower limit assuming k=1. We generated 10,000 random samples from N(1,7), normal distribution with mean = 0 and variance =7; Exp(7), exponential distribution with rate parameter λ =7; and chi-squared distribution χ² (1), degree =1. We compare the discrepancy between the probability of coverage probability greater than the pre-specified 0.90. The results are given in Figures 1, 2 and 3. In Figures 1 to 3, Half-Half stands for the average of the two order statistics, Proportion (p) stands for the interpolation of two order statistics, Proportion (s) stands for the interpolation of order statistics based on the sample sizes. In addition, the determination of lower and upper limits without interpolation are also presented in those figures, which are labeled by Lower and Upper, which stands for the smaller order statistics and the larger order statistics, respectively. For example, with sample size = 150, for a tolerance interval of 95% coverage and with 95% confidence level, then X₍₁₎ would be chosen as the lower limit under the approach of Lower; X₍₂₎ would be chosen as the lower limit under the approach of Upper.

Discussion and Conclusion

[1] Propose to use the “goodness” criterion proposed by [6] to determine the sample size for two one-sided tolerance intervals for product quality specifications. More specifically, it is proposed to use δ=(1-p)/4 for the “goodness” criterion. When the data are continuous but following unknown distribution, typically the tolerance interval is estimated using order statistics. We adapt Wilks’ proposal of using order statistics to determine the limit of the one-sided tolerance interval [2]. Based on Wilks’ method, we can determine the minimum sample size requirements for one-sided and two one-sided tolerance intervals with a targeted order statistic as the limit(s). Furthermore, we adapt the interpolation of order statistics approach proposed by [8-11] to improve the precision of the estimate. We also propose to use interpolation method to determine the limits of tolerance interval for sample sizes not presented in the minimum sample size tables. Through a simulation study, we have demonstrated that both methods can improve the precision of the estimated nonparametric tolerance intervals with more accurate coverages given certain confidence levels.

In the future research, we will use formula (4) to construct of the lower limit of the lower confidence limit of percentile estimation. It leads to the determination of the cut point in immunogenicity studies. It can further be used for testing the difference of percentiles of two distributions and assessing the comparability of biologic products.

Acknowledgement

The authors want to acknowledge the contributions of Drs. Atiar Rahman, Chao Wang, Yu-Ting Weng, Xiaoyu Cai, Shaobo Liu, Xutong Zhao and Tengfei Li of FDA in participating in the discussion during the development of the procedure.

Supplementary Material