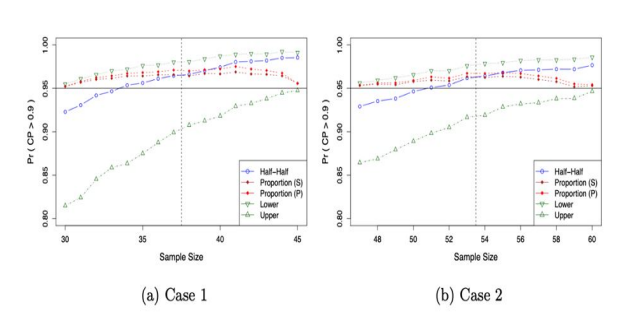
Figure 1: Determination of Nonparametric Lower Tolerance Limits when the Underlying Distribution is N(1,2): True Probability of Coverage Probability greater than 0.9 depending on Sample Size
Risk Group |
Reasons |
Reference |
Pregnant women |
Methionine is metabolised to homocysteine and raised plasma homocysteine is associated with birth defects, pre-eclampsia, spontaneous abortion and placental abruption. |
15, 16 |
Schizophrenic patients |
Schizophrenic patients given 10–20 g methionine daily developed functional psychoses. |
17 |
Patients with pre-existing cancer |
Animal studies have shown that restriction of methionine intake blocks division and metastasis of tumour cells. |
18,19 |
Ischaemic heart disease (IHD), peripheral vascular disease (PVD), stroke |
Methionine is metabolised to homocysteine – raised homocysteine levels are associated with IHD, PVD and stroke. |
20-22 |
Patients with chronic liver disease |
The liver has an impaired ability to metabolise methionine. |
22 |
Table 1: Nonparametric Two One-sided Tolerance Intervals: Sample Size Requirements so that
For one-side tolerance interval (p, 0.95) for p=0.8, 0.9, 0.95 and 0.99 can also be calculated with formula (7). The results are given in Table 2.
α= 0.05 |
||||
Values of k |
p =0.8 |
p =0.9 |
p =0.95 |
p =0.99 |
1 |
14 |
29 |
59 |
299 |
2 |
22 |
46 |
93 |
473 |
3 |
30 |
61 |
124 |
628 |
4 |
37 |
76 |
153 |
773 |
5 |
44 |
89 |
181 |
913 |
6 |
50 |
103 |
208 |
1049 |
7 |
57 |
116 |
234 |
1182 |
8 |
63 |
129 |
260 |
1312 |
9 |
69 |
142 |
286 |
1441 |
10 |
76 |
154 |
311 |
1568 |
11 |
82 |
167 |
336 |
1693 |
12 |
88 |
179 |
361 |
1818 |
13 |
94 |
191 |
386 |
1941 |
14 |
100 |
203 |
410 |
2064 |
15 |
106 |
215 |
434 |
2185 |
16 |
112 |
227 |
458 |
2306 |
17 |
118 |
239 |
482 |
2426 |
18 |
124 |
251 |
506 |
2546 |
19 |
129 |
263 |
530 |
2665 |
20 |
135 |
275 |
554 |
2784 |
Table 2: Nonparametric One-sided Tolerance Intervals: Sample Size Requirements so that X(k) is the Lower Tolerance Limit or X(n-k+1) is the Upper Tolerance Limit
α= 0.05 |
||||
Values of k |
p =0.8 |
p =0.9 |
p =0.95 |
p =0.99 |
1 |
14 |
29 |
59 |
299 |
2 |
22 |
46 |
93 |
473 |
3 |
30 |
61 |
124 |
628 |
4 |
37 |
76 |
153 |
773 |
5 |
44 |
89 |
181 |
913 |
6 |
50 |
103 |
208 |
1049 |
7 |
57 |
116 |
234 |
1182 |
8 |
63 |
129 |
260 |
1312 |
9 |
69 |
142 |
286 |
1441 |
10 |
76 |
154 |
311 |
1568 |
11 |
82 |
167 |
336 |
1693 |
12 |
88 |
179 |
361 |
1818 |
13 |
94 |
191 |
386 |
1941 |
14 |
100 |
203 |
410 |
2064 |
15 |
106 |
215 |
434 |
2185 |
16 |
112 |
227 |
458 |
2306 |
17 |
118 |
239 |
482 |
2426 |
18 |
124 |
251 |
506 |
2546 |
19 |
129 |
263 |
530 |
2665 |
20 |
135 |
275 |
554 |
2784 |
The coverage p for a given tolerance interval (X(k),X(n)) or (X(1),X(n-k+1)) for a given k and n can also be calculated. The true coverage p (with 95% confidence level) for selected k and n are given in Table 4.
Table 3: Nonparametric Two One-sided Tolerance Intervals: True Coverage Probability (p) for a given Lower Tolerance Limit (X(k),X(n-k+1))
Sample Size |
Values of K |
|||||||||
Size |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
20 |
0.860 |
0.783 |
0.717 |
0.656 |
0.598 |
0.544 |
0.492 |
0.441 |
0.393 |
0.346 |
25 |
0.887 |
0.823 |
0.768 |
0.718 |
0.670 |
0.624 |
0.580 |
0.537 |
0.496 |
0.456 |
30 |
0.904 |
0.851 |
0.804 |
0.761 |
0.720 |
0.681 |
0.642 |
0.606 |
0.570 |
0.534 |
35 |
0.917 |
0.871 |
0.830 |
0.793 |
0.757 |
0.722 |
0.689 |
0.656 |
0.625 |
0.594 |
40 |
0.927 |
0.886 |
0.850 |
0.817 |
0.785 |
0.754 |
0.725 |
0.696 |
0.667 |
0.640 |
45 |
0.935 |
0.898 |
0.866 |
0.836 |
0.808 |
0.780 |
0.753 |
0.727 |
0.702 |
0.676 |
50 |
0.941 |
0.908 |
0.879 |
0.852 |
0.826 |
0.801 |
0.776 |
0.753 |
0.729 |
0.706 |
60 |
0.951 |
0.923 |
0.898 |
0.875 |
0.853 |
0.832 |
0.812 |
0.792 |
0.772 |
0.752 |
70 |
0.958 |
0.934 |
0.912 |
0.892 |
0.873 |
0.855 |
0.837 |
0.820 |
0.803 |
0.786 |
80 |
0.963 |
0.942 |
0.923 |
0.905 |
0.889 |
0.873 |
0.857 |
0.841 |
0.826 |
0.811 |
90 |
0.967 |
0.948 |
0.931 |
0.916 |
0.901 |
0.886 |
0.872 |
0.858 |
0.845 |
0.831 |
100 |
0.970 |
0.953 |
0.938 |
0.924 |
0.910 |
0.897 |
0.885 |
0.872 |
0.860 |
0.848 |
120 |
0.975 |
0.961 |
0.948 |
0.936 |
0.925 |
0.914 |
0.903 |
0.893 |
0.882 |
0.872 |
140 |
0.978 |
0.966 |
0.955 |
0.945 |
0.935 |
0.926 |
0.917 |
0.908 |
0.899 |
0.890 |
160 |
0.981 |
0.970 |
0.961 |
0.952 |
0.943 |
0.935 |
0.927 |
0.919 |
0.911 |
0.903 |
180 |
0.983 |
0.973 |
0.965 |
0.957 |
0.949 |
0.942 |
0.935 |
0.928 |
0.921 |
0.914 |
200 |
0.985 |
0.976 |
0.968 |
0.961 |
0.954 |
0.948 |
0.941 |
0.935 |
0.928 |
0.922 |
When an experimenter wants to determine the lower and upper limits of the specification that covers at least 90% of the product population, for a continuous attribute with unknown distribution, he needs to plan an experiment with at least sample size of 72. On the other hand, for k=1, (X(k),X(n-k+1)) is the range of minimum to maximum (table1). With sample size n=35, the range determined by (min, max) is 80% of the population centered at median (table3).
Table 4: Nonparametric One-sided Tolerance Intervals: True Coverage Probability (p) for a given Lower Tolerance Limit X(k) or Upper Tolerance Limit X(n-k+1)

Figure 1: Determination of Nonparametric Lower Tolerance Limits when the Underlying Distribution is N(1,2): True Probability of Coverage Probability greater than 0.9 depending on Sample Size
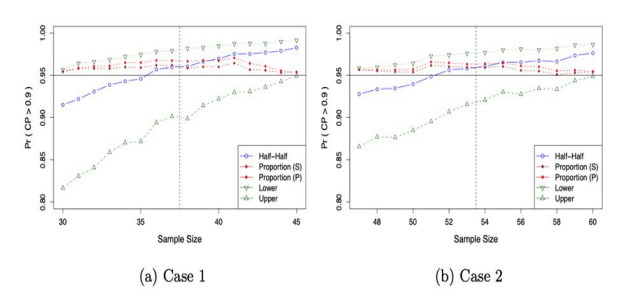
Figure 2: Determination of Nonparametric Lower Tolerance Limits when the Underlying Distribution is Exp(0.7): True Probability of Coverage Probability greater than 0.9 depending on Sample Size
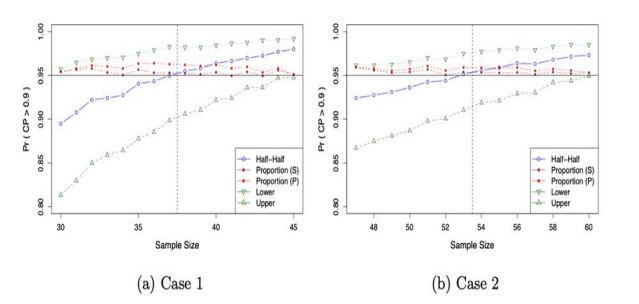
Figure 3: Determination of Nonparametric Lower Tolerance Limits when the Underlying Distribution is chi-square (1): True Probability of Coverage Probability greater than 0.9 depending on Sample Size
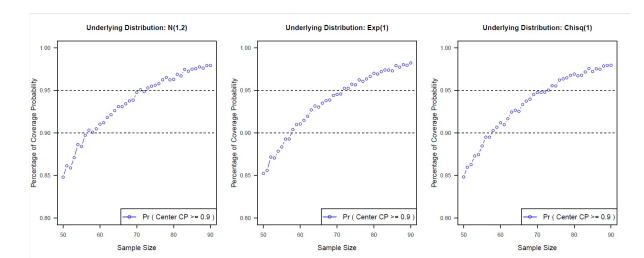
Figure 4: Simulation results for the (P,1-a) nonparametric two one-sided tolerance interval (X(k),X(N-k+1)) when k = 1, a = 0.05. The figure below presented the center coverage of the tolerance interval for different sample size N under three types of underlying distributions. The minimum sample size requirement to obtain a center coverage greater than 0.9 is consistent with the results in Table 1 with k = 1 and P = 0.9.
Tables at a glance
Figures at a glance