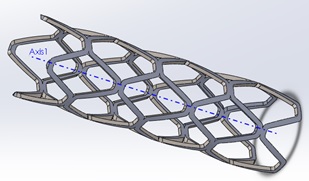
Figure 1 3D model of 8-sturt structure stent with 4 rhombus cross-sectional units

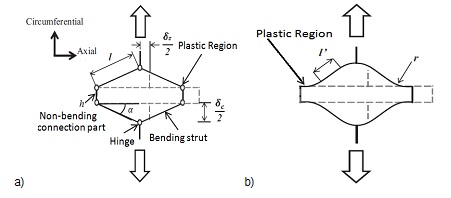
Figure 2 Nonlinear analysis approach for stent with rhombus structure considering the connection part of model a) idealized analytical model in non-linear analyses b) part curvature of plasticity region due to the expansion forces [16].

Figure 3 Non-uniform artery geometry [1]

Figure 4 3D artery model with blood flow developed from IVUS image

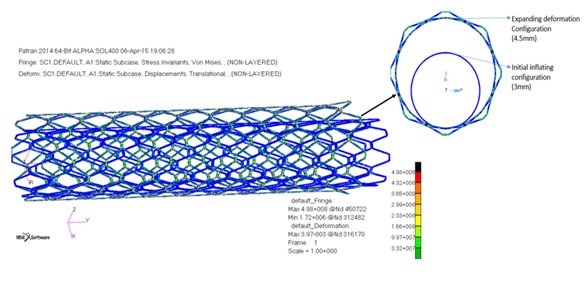
Figure 5 Stress distribution of inflated stent under pressure from 3mm (blue configuration) to 4.5 mm (green configuration)

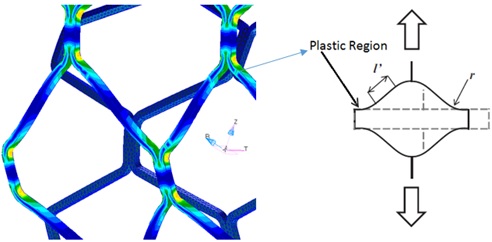
Figure 6Stent configuration after inflation showing the plastic regions with the maximum equivalent stress presented with yellow/green colors and aligns with the theoretical model

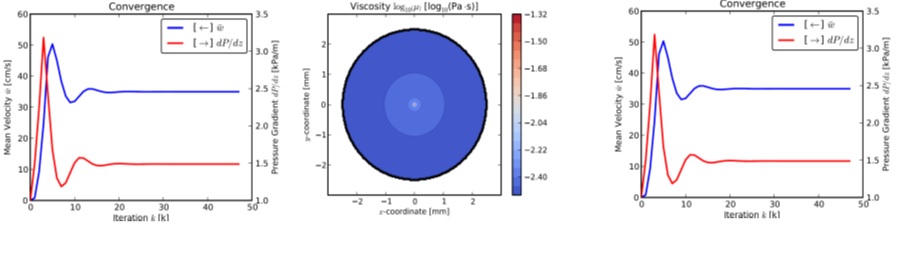
Figure 7 a) Velocity distribution of the blood flow in artery cross-section b) viscosity distribution of the blood flow in artery cross-section c) Comparison of the mean velocity and pressure gradient over several iterations

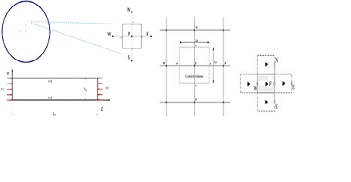
Figure 8 a) Segment of blood model field (cross-section of the artery) as the control volume of studied flow. b) finite volume cell with neighbor points in the control volume.

Property	Value
Young’s modulus	190GPa
Poisson ratio	0.3
Yield stress	207MPa
Ultimate stress	515MPa
Limit nominal strain	60%

Table 1. Materials properties of 316L SS stents

Parameter	Calculated Value
Power law index in Carreau model (n)	0.344
Zero shear rate limit (μ_0)	0.0456Pa
Infinite shear rate limit(μ_∞)	0.0032 Pa
Relaxation time constant(λ)	10.03s
Ideal mean velocity of blood	0.35 m/s

Table 2. Parametric values for the non-Newtonian constitute equations