Full Text Article

Introduction

Bone assessment, and in particular trabecular bone (TB), using Ultrasound (US) methods, are nowadays faster, less expensive, with higher portability and simpler than their counterparts in the x-ray regime. Here are included quantitative computed tomography (QCT) and dual-energy x-ray absorptiometry (DEXA). Studies were performed with regard to properties of a TB and the e of US propagation through it [1,2].

The US diagnostic capabilities for predicting fractures risks were documented in studies, such as in calcaneal broadband US attenuation (BUA) and similarly for TB’s speed of sound (SOS) [3, 4]. These two parameters highly correlate with calcaneal bone mineral density (BMD), which serves also as an indicator for osteoporotic fracture risk. e BUA and SOS were also found as an indicator of osteoporotic fracture risk in the hip [3,4].

The US attenuation in TB was analyzed at several frequency bands, between 0.2 to 1.7 MHz. It was found experimentally that the linear dependence of attenuation on frequency is up to 1.7 MHz.

It was found that a linear combination of BUA and SOS are of greater diagnostic capability than either parameter by itself, as it was demonstrated to be predictive of hip and other fractures in women in prospective studies [4].

From previous investigations it is known [5-10] that US backscatter provides information with regard to size, shape, density and elastic properties of scatterers

Similar studies were performed using computer simulation of the scattering process in TB [11-13], where the simulation was based on Finite e Time Domaine (FDTD) method. e data obtained from simulation was compared with those obtained by ‘High Resolution Synchrotron Radiation Micro Tomography’. Two quantitative ultrasound parameters were studied at 1MHz, for both - simulated and experimental signals: the normalized slope of the frequency dependent attenuation coefficientt (also known as ‘normalized broadband ultrasound attenuation’ (nBUA) in the medical field), and the ‘phase velocity’ at the center frequency. It was shown in these studied [12,13] that the simulated and experimental nBUA are in close agreement, especially for specimens with high porosity. For specimens with a low porosity (or a high solid volume fraction), the simulation systematically under-estimated the experimentally observed nBUA. s result suggests that the relative contribution of scattering and absorption to nBUA may vary with the bone volume fraction.

A linear relationship was found between experimental and simulated phase velocity, where the last one was found to be slightly higher than the experimental one; may be explained by the choice of material properties applied in the simulation.

The diminished number and thicknesses of trabeculae within bone that are associated with increased fracture risk, would be expected to reduce the backscatter. Several studies have established diagnostic promise and clinical feasibility of these measurements [5,8-10]. A possible explanation for this apparent inconsistency was found that the US measurements may provide some independent information regarding structure that is not contained in usually applied parameters, but used to describe microarchitecture (such as: mean trabecular thickness, mean trabecular number, mean trabecular spacing, bone volume to total volume ratio, bone surface-to-volume ratio, number of nodes and degree of anisotropy).

It was also investigated [3, 4] that the degree to which calcaneal backscatter measurements can be applied for predicting its BMD, where a high predictive value suggests linear combinations of US parameters that can be used instead of BMD. Other predictive values are described in [3,4].

In the present study, attention was paid to the analysis of US transmitted (Tr) signals through a TB sample. , experiments were performed on three TB samples with different thicknesses.

In transmission (Tr) type of measurements are required two US transducers, mounted usually on the opposite sides of the sample, where one acts as a transmitter (Tr) and the other - as a receiver (Rc). e experiments performed include:

(i) Assessing the speed of sound (SOS) and attenuation in TB slices and calculating their spectral response distribution (performed by means of The Fourier transform (FT) of the signal where it identifies its frequency components. (In MATLAB®, the Fast Fourier Transform (fft) function computes the FT using a fft algorithm. Thus, the fft is used to compute the discrete FT of the signal – the method that was applied here). These spectral distributions were performed on the transmitted and received signals

(2) Spectral response of the received signals for:

(a) several US Tr frequencies and

(b) the number of pulses per burst.

(3) Sensitivity of SOS related to the positions of the US transducers, by comparing measurements of their opposite positions.

As a summary of the described measurements, it was observed:

(i) the attenuation is more significant at higher frequencies, as expressed also in their spectral responses;

(2) Similar observations of attenuation were obtained while transmitting higher US frequencies

(3) Similar results were obtained also for the SOS assessment while it was performed it in opposite directions on the same slice.

Methods and Materials

There were performed US transmission (Tr) measurements on three samples of a TB.

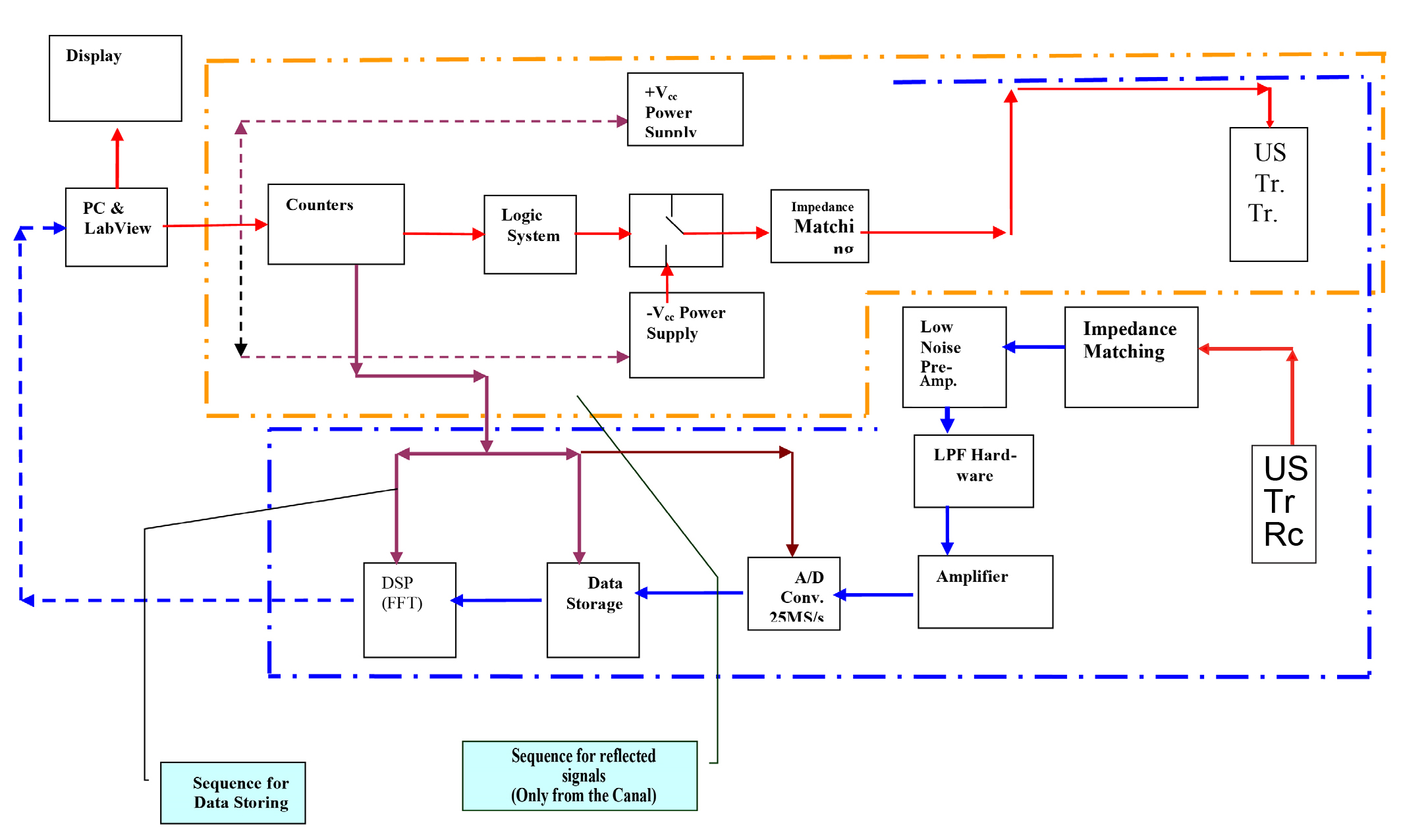
Figure 1 describes the experimental configuration for a Tr mode measurement, where two US transducers were applied – one for Tr of the US signal and the other – for its reception (Rec).

Block Diagram Explanation

The measuring system consists of the following:

(1) The transmitter branch (red limes with arrows) that end with the US transducer that transmits the pulsed signals into the sample under test.

(2) The receiver branch (blue lines with arrows) that starts with the US transducer that receives the signals that propagate through the sample under test.

(3) Amplifying and converting the received analog signals to digital one and storing it.

(4) Performing a DSP, including FFT (using the dedicated MATLAB software) and

(5) Displaying the resultant computation.

Description of the Transmitter

The main logic system

It controls the operation of the transmitter: the "Logic system", High voltage power supplies; and in the receiver: the "A/D converter", sequences for recording the transmitted signals on the "Data Storage", and sequences for the DSP.

The NI-6602 (of National Instruments) was chosen, it contains 8 clocks and operates with the LabView software.

Logic System

The logic system is a part of a board obtained from Supertex (1711DB1). The 'logic system' on this board is a product of Xilinx, Mod. XC9752-XL-VQ44.

Fast Switching Device

This device is composed of two identical channels, where each one of them contains a control logic and level translator (Supertex MD1711) and the fast-switching device (Supertex TC6320)

According to the specifications of the fast-switching device:

* The output sink resistance is 6 ohms, for a current of Isink = 100mA.

* The Peak output sink current is 2A

* TC6320 Minimum HV Negative Supply = -100V

* TC6320 Maximum HV Positive Supply = 100V

* The propagation delay when output is from low to high (or from high to low) = 19nsec, without a load

* Output rise-time = output fall time = 8nsec, with a load of 1nF

* Delay time matching = ±3nsec

* Output jitter = 30ps

Power Supplies

The switches are fed by two power supplies of Nemic-Lambda, type ZUP120-1.8. One of them will supply +100V and the other -100V. Both of them will be able to supply a current of 1.8A.

Description of the Receiver

The receiver contains the following sub-systems (See Fig. (2)):

Low impedance (50 ohm) , RITEC,type PAS-01-55-LZ, # 4659

Since it is a low impedance input unit, its input noise level is relatively low, according to the Johnson's law:

Therefore, the Minimum Detectable Signal (MDS) is about 10 μVrms.

The low input impedance of approximately 50 ohms is shunted by a 20pF capacitor.The gain of the pre-amplifier is switch selectable from a gain of 20 dB, 30 dB and 40 dB.

The output impedance of the pre-amplifier is 50 ohms.

The 1^st stage of the pre-amplifier consists of a pair of low-noise junction-type FET's in a cascade configuration. The 2^nd stage is a clamped output, current feedback operational amplifier with extremely fast recovery from overload conditions.

The low frequency 3 dB point is determined by the inductor L2 = 470 μHenries, while the high frequency 3 dB point is determined by the selected gain and the stray capacity of the circuitry in shunt with the FET load resistor R16 = 51 ohms. The high frequency 3 dB point will decrease in frequency as the gain is increased from 20 dB to 40 dB. The 3 dB bandwidth points occur at frequencies of approx. 50 kHz and 80 MHz, for gain settings of 20 dB and 30 dB, and approx. 50 kHz and 55 MHz for a gain setting of 40 dB.

Band-pass filter

RITEC, type RBPF, # 4661 is inserted in the receiving circuit, in order to filter the received signal in the range of the measured frequencies

According to the specifications, its 3dB points are at 2.89 MHz and at 9.54 MHz.

High impedance amplifier, RITEC, PAS-01-40-1K, # 4658.

Its rms noise voltage, according to eq. 1, is approximately 8.8 μV_rms, which means an MDS of 45 μV_rms.

The input impedance is approximately 1 Kohms, shunted by a 20pF capacitor. The gain of the pre-amplifier is switch selectable from a gain of 20 dB, 30 dB and 40 dB. The output impedance of the pre-amplifier is 50 ohms.

The 1^st stage of the pre-amplifier consists of a pair of low-noise junction-type FET's in a cascade configuration. The 2^nd stage is a clamped output, current feedback operational amplifier with extremely fast recovery from overload conditions.

The low frequency 3 dB point is determined by the inductor L2 = 470 μHenries, while the high frequency 3 dB point is determined by the selected gain and the stray capacity of the circuitry in shunt with the FET load resistor R16 = 51 ohms. The high frequency 3 dB point will decrease in frequency as the gain is increased from 20 dB to 40 dB. The 3 dB bandwidth points occur at frequencies of approx. 50 kHz and 80 MHz, for gain settings of 20 dB and 30 dB, and approx. 50 kHz and 55 MHz for a gain setting of 40 dB.The 3

A/D Converter

An A/D system – GaGe CompuScope, type 14400,was chosen.

Details of the Transducers

(1) In the t experiment, the transducers we applied: Panametrics, type C310 (fr = 5 MHz) and Piezo-Technologies, ( fr = 7.5 MHz);

(2) In the second and third experiments, the following transducers were applied:

Panametrics, type C310 and Piezo-Technologies, both for (f_r = 5 MHz).

The TB samples and their preparation

The TB was obtained from a hip of a porcine and received from a slaughterhouse, where it was also prepared according to our directions: using a fine saw for slicing the samples, and cutting/slicing it very slowly – in order that the surface will remain as smooth as possible.

Three TB samples were measured mechanically, with a measuring accuracy of 10^-2 mm.

Each sample was measured 10 times and the mean value with the Standard Deviation (STD) were calculated.

The slices thicknesses were as follows:

Slice 1: 8.3mm; Slice 2: 14mm and Slice 3: 4.5mm.*

Where the STD was smaller than 0.1 mm in all the 3 samples

*Approximated thickness, as its surfaces (where the US transducers are attached) were not as flat, as in the other two slices. This irregularity caused to a difficulty to perform an accurate measurement and defining its thickness with a similar accuracy as of the other two samples.

Experiments

Experiment 1

The following was performed in this experiment:

(1) Assessing the US SOS in TB, for a Tr mode.

(2) Monitoring the attenuation (Att) as a function of frequency, for Tr and Rec signals; and

(3) Investigating the t of reversing the measuring direction on the SOS in TB, while applying a Tr mode.

Experimental Procedure

Three TB samples with different thicknesses, were applied in this experiment.

Their thicknesses were measured mechanically, by a caliber.

Two transducers were assembled on the sample, opposite to each other - as shown in Fig. 1.

The US Rec signals were detected by an US transducer.

The output of the Rec transducer was connected directly to the oscilloscope (that includes a pre-amplification stage).

Method for Assessing the SOS in TB slices

(1)The amplitude of the recorded signal was measured.

(2)The TB slice under test (between the two transducers) was removed and the received US signal amplitude was measured directly through water.

Calculating the relative attenuation between these two measurements.

Note: In the following experiment the US Panametrics transducer (f_r = 5 MHz) was applied as the transmitter (T_r), while the Piezo-Technologies (f_r = 6MHz) as a Rec.

Examples of Signals as a Function of Time and Frequency

(i) Tr and Rec signals, f_US = 5 MHz, 1 pulse/burst

Since all three slices were obtained from the same hip, it does not seem reasonable that the trabecula’s orientation in this particular sample, are in different direction – causing to higher attenuation.

(ii) Attenuation vs. frequency measurements, for T_r of 1 pulse/burst

(iii) Transmission of 6 pulses per burst

(1)the spectral response of the Tr signal (6 pulses/burst) and of the Rec signal, presented for the 3 slices

Assessing the Speed of Sound (SOS)

The SOS in a specific slice was assessed from the knowledge of the distance x (thickness of the slice) [m] and time t (the time between the transmitted pulse and the received signal [sec]).

Applying the formula for velocity: c=x/t, where c is the SOS in TB slice[m/sec] and t is the time [sec] that the US signal travelled through the TB slice.

These calculations are summarized for two slices in Table 1:

Experiment 2

The following was performed in this experiment

(1) Assessing the SOS in TB.

(2) Analysis the attenuation vs. frequency, in TB.

Method

(i) e experiments were similar to those of ‘Experiment 1’, except that here we replaced the US transducers tasks (i.e., Tr signals were obtained from the US transducer type Piezo-Technologies f_US =5 MHz, and the Rec signals - by US transducer Panametrics).

(ii) All the experiments in this section were performed with one slice of TB, thickness of 12.9 mm

Examples of Signals vs Time and their Spectral Responses

(1) Tr at 5 MHz, 1pulse/burst:

(ii) The spectrum of Tr and Rec signals, at 5 MHz, 1 pulse/burst

(1) Tr vs. time, at 5MHz, 6 pulses/burst

(iv) Spectral responses of Tr and Rec signals, at f_US = 6 MHz, for 3 pulses/burst

(v) Tr vs. time, at fUS = 6 MHz, 6 pulses/burst

Experiment 3

Purpose

The purpose in this experiment was to find out if the opposite direction of TB fibers affects the SOS value.

Method

Two slices were applied in this experiment; They were prepared by applying a fine saw, in order to obtain these planes smooth. The two US transducers were attached against those two smooth planes, in opposite directions.

A single measurement was performed, applying an oscilloscope with V-bars option, enabled to determine the time difference between the Tr and the Rec signals.

Results

The slice thickness was: Δx= 8.4 mm, and the time difference between the transmitted and received signals was: Δt = 5.44 μsec.

Accordingly, the velocity in the TB slice was: v = 1544 m/sec.

There is no significant difference between this result and those obtained in experiment 1 (a difference of 2.2%).

Therefore, it can be concluded that in a Tr measuring method, there is no significant difference in the SOS, related to the measuring direction.

Results and Discussion

Presented are experiments with the 3 TB slices of different thicknesses, using a Tr US pulsed mode for assessing the SOS and attenuation. The US Tr was at frequencies of 4, 5 and 6 MHz, containing 1, 3 and 6 pulses/burst

In Fig. 3, one can see the delay (time difference) in the Rec signal, as related to the Tr one and it is proportional to the TB slice thickness, i.e. the path-length of the US Tr signal (until it arrives to the detecting US transducer). These time delays are proportional to the slice thicknesses (within a measuring error and inhomogeneity of the slices).

Regarding the Rec amplitudes (peak-to-peak) – the evaluated relative attenuation in a TB sample, is summarized in Table 2.

Conclusions

(1) The SOS in TB was assessed about 1500 m/sec and changes ~2% between the TB samples.

(a) Although the Tr frequency in these experiments was between 4 to 6 MHz, the spectrum of the Rec signal shows a strong dominance for low frequencies, which was in most cases between 1 to 3 MHz. s result leads to a conclusion that the TB attenuates less the lower frequencies than the higher one.

There is a linear relation between the attenuation coefficient and frequency, leading to an exponential drop in intensity of the received signal, expressed as: `I(Δx) = I0*exp (-α *Δx) (assuming there are no reflections, or they are negligible).

Since low frequencies are contained in the first and last pulses of a burst (due to the transducer excitation and relaxation properties), the received signal presents two large amplitudes - which are the first and last pulses in the burst, while between them smaller amplitudes exist - they correspond to the Tr frequency domain.

(1) From Table 1 and the results of experiment 3, it turns out that the SOS in the TB is not sensitive to the measuring direction, while using the Tr mode (the two US transducers are applied in a certain direction, or in the opposite one).

(2)The spectral coherence method and particularly the spectral analysis of the Tr and Rec signals provide a more general information on the way that the US signal is at the entrance and at the output of a TB sample. From here, for example, attenuation vs frequency can be obtained

(3) Measurements with sample 2 were not as correct as with the other two samples, due to the relative roughness of the sample, where the US transducers were attached. This can be prevented by preparing (while cutting the slice) the surface more smoothly.

(4) As the SOS and attenuation are important parameters of a TB [3. 12], the method presented here, provides these parameters using methods if signal processing thus providing simultaneously the TB response at a wide frequency band.

Acknowledgment

Our thanks to Mr. Ilan Vinkle and Mr. Yechiel Lamesh for their help while performing the experiments.