Full Text Article

Introduction

We are currently in the age of advanced artificial intelligence that is, a machine able to react or to think like a human being [1]. In order to do this, it requires an enormous amount of information, both to train itself and to make decisions [2]. This information is obtained by analyzing a huge amount of data, or a database. There are several types of information in the literature, but what interests us most is information of the association rules type. Association rules is an information presented like , that we can read as if X is present or true then Y will be present or true. This kind of information can help us to take a decision in more fields interacting with decision making even in medical health, social sciences, environment, more other [3]. In this article, we present what an association rule is and how its quality is measured. We then present and analyze two measures of association rules: the McNemar and M_GK.

Association Rules and their Measurements

An association rule is a pair (X,Y) noted where X and Y are disjoint patterns (or conjunctions of binary variables). An association rule of type association rule takes the form "If condition, then result". It has a premise part (or antecedent) composed of a set of variables X and a conclusion part (or consequent) composed of a set of variables Y disjoint from X. Such a rule is used to discover whether transactions that verify pattern X tend to verify pattern Y as well. For this reason, it is extracted from a formal database, as defined below. An association rule is entirely characterized by its contingency table, which is the basis for calculating association rule evaluation measures.

Definition 2.1: Formal Database

Let a set of m variable items or attributes, and a set of n transactions or entities defined on the set of attributes. A subset is the set of parts of A) is called a pattern and its complement. Each transaction t_i consists of forming a subset of attributes of A,X_k. A transaction is said to t_i satisfies x_k if the transaction t_i contains x_k in which case we write t_i[x_k]=1 otherwise t_i[x_k]=0. A transaction contains a pattern if all the attributes that make up the pattern are contained in the transaction. The triple (T,A,R), where T is the set of transactions or objects, A the set of attributes or variables and R a binary relationship from T to A [7].

Definition 2.2: Pattern extension

Let K = (T,A,R) be a binary data mining context. The extension of the pattern X denoted X^’ the set of t of T such that for all x from X, tRx:

In the set of transactions, which we have denoted T we can define a discrete probabilized space (T,P(T),P) where P is the discrete uniform probability [4].

In health study, as used in “Improved extension of MGK in several premises simplified applied on COVID19 study” [5], the motif X can represent the symptoms, Y a disease and X^’ is a list of all patients presenting the symptoms X.

So, if . If X and Y being two patterns such where α is a predefined value indicating the significance of the combination (X,Y). From these significant combinations, we can build an association rule such as or .

Definition 2.3: Formal definition of an association rule

An association rule of a formal context K = (T,A,R) is a pair (X,Y) noted where X and Y are patterns and is commonly read as "if X, then Y". It expresses an association or oriented link between X and Y, and X is said to be the premise and Y the consequent.

According to these definitions, an association rule is generated from a large database, which we have called a formal database. As a result, many association rules can be generated, but not all of them can be considered significant. To assess their significance, we need to use a reliable sorting tool, known as a probabilistic measure of interest. At present, there are several such measures, for example: Confidence, Lift, positive predictive values (PPV), negative predictive values (NPV), Odd-Ratio, the McNemar test, etc., around one hundred and nine (109), in the literature. The large number of measures is due to the fact that researchers are striving to improve the measures in order to have confident and reliable association rules. A study leaded by Bruce [6] has shown the shortcomings of the Odd-Ratio test compared with the M_GK test. This means that we try to find a good measure that can give us the best result. In the reminder of this article, we will compare the McNemar measure with the M_GK measure, which has already overtaken the Odd-Ratio measure. However, a measure must respect some forms and conditions.

Definition 2.4 (A quality measure: µ).

Let be patterns. A probabilistic quality measure is a real function µ of such that for any association rule is a real value calculated from the four quantities: , where P denotes the discrete uniform probability on the probability space (A,P(A)).

Property 2.1 (Measure property).

1. A measure is said to be symmetrical if .

2. A measure is said to be oriented if there is at least one association rule we have .

Several researchers have focused on the criteria for evaluating a good quality measure (André Totohasina in 2008 [7], Lenca Philippe in 2011 [8], Grissa in 2013 [9], Lan Phuong in 2016 [10] and Rakotomalala in 2019 [11], among these works, we were able to select some criteria:

• Measurement comprehensibility for the user (interpretable);
• Nature of the rules targeted by the measure;
• Sensitivity to the appearance of examples and counter-examples;
• Direction of measurement variation;
• Type of variation: linear/non-linear;
• Impact of the scarcity of the consequent;
• Sensitivity to data size;
• Discriminant character of the measurement;
• Use of a pruning weir;
• Measurement-induced classification
• Contextual behavior of the rules studied;
• Deviation from equilibrium;
• Contradiction of the user's priori knowledge;
• Noise sensitivity.

According to the literature, measures that meet most of these criteria are ranked better than others. In what follows, we will not compare them on the basis of these criteria, but rather on their mathematical expressions.

McNemar's Measurement

The McNemar measure, generally used in the McNemar test, is often used to evaluate the dependence of two binary qualitative variables, or of the same variable evaluated under two different conditions or instants [12]. In her article entitled: "Matched analysis for paired binary data (McNemar test)" published in the American Journal of Orthodontics and Dentofacial Orthopedics (AJO-DO), Despina Koletsi presented an application of the McNemar test to the identification of early root resorption of lateral incisors [13]. For his part, Jean Claude Regnier used the McNemar test to assess the dependence of students' responses to exercises [14].

Definition 3.1: Definition of the McNemar test

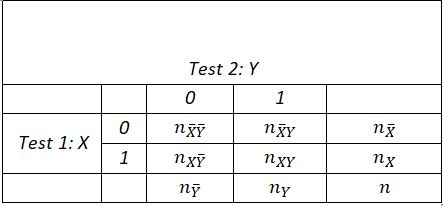
Consider the following contingence table (Table 31):

Interpreting table values in Table 31:

: number of individuals who answered 0 (or absence of X) in test 1 and 0 (or absence of Y) in test 2

nXY: number of individuals who answered 1 (or presence of X) to test 1 and then 1 (or presence of Y) to test 2

: number of individuals who answered 0 (or absence of X) to test 1 then 1 (or presence of Y) to test 2

: number of individuals who answered 1 (or presence of X) to test 1 and 0 (or absence of Y) to test 2

McNemar's measure is defined by [12].

This expression follows a chi-square distribution with one degree of freedom and α risk threshold. Remember that in the definition of a measure (definition 2.4), it should be expressed in terms of four elements: .

So, let's re-express McNemar's measure in accordance with the indications for formulating the measure. We then have the following proposition.

Proposition 3.1:

Let X and Y be two patterns, P() the uniform probability. The McNemar measure applied to the association rule is defined by:

Proof

Given that X and Y are patterns in a formal database K = (T,A,R), we can define a probabilized space on the formal database K with uniform probability, such that .

Multiply the numerator by and the denominator by then we have:

We know that

The same goes for

We then have

Note: In this new expression of the McNemar measure the measure is therefore symmetrical.

A McNemar test validation use the chi-square table with one degree of freedom.

MGK Measurement

The MGK interest measure of association rules goes by various names independently, depending on the researcher and the year of its discovery: inspired by the Loevinger index, MGK (Guillaume-Kenchaff measure) was independently proposed and named in 2000 by Guillaume" ION (Implication Oriented Normalized) in 2003 by Totohasina, CPIR (Conditionnal Probability Incrementation Ratio) in 2004 by Wu and Zhang, verifying the oriented implicative property of Brin and his team in 1997 [15]. Due to the expression of a minimum condition and efficiency ratio for extracting non-redundant rules, this measure is both more accurate and comprehensible. By definition, the MGK measure is expressed as:

Indeed

- if X favors Y, on the one hand

so

on the other hand

so

so

So

• if X disfavors Y, on the one hand

So

and on the other hand

so

so

so

If we denote by called the favorable component, and called the unfavorable component, then the measure MGK can be expressed

Measurement Reference Situations M_GK

A definition of reference situations is a criterion justifying the quality of a measurement. The MGK measure presents these situations [7,11] as follows:

Incompatibility: X and Y are incompatible if and only if .

Unfavorable situation or negative dependency: X disfavor Y if and only if .

Situation of independence: X and Y are independent if and only if

Favorable situation or positive dependence: X favor Y if and only if .

Logical implication situation: X logically implies Y if and only if

Equilibrium situation: in an equilibrium situation, i.e. , the measurement M_GK = ±1/2

Measurement validation threshold M_GK

Like all the measures we have seen above, the M_GK measure has a slightly different validation threshold: it is calculated using the Chi-square statistic, based on the principle of assigning confidence to the rules that will be generated. The M_GK threshold is expressed as:

An association rule is therefore valid, according to the measure M_GK if the absolute value of its M_GK is greater than the absolute value of the threshold M_GK threshold (α) and this, at a confidence level 1- α.

Comparative Analysis of McNemar and M_GK

By definitions,

And

As the both measures are expressed with , we can express each with other, it means . Considering, , we have the following relation:

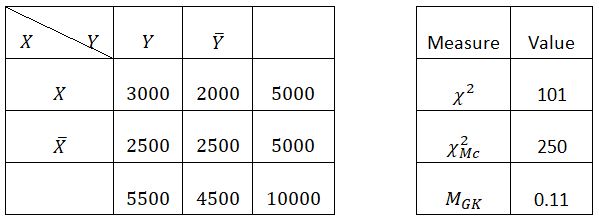
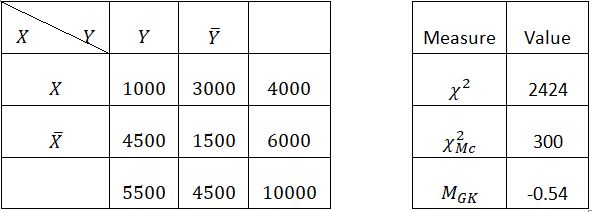
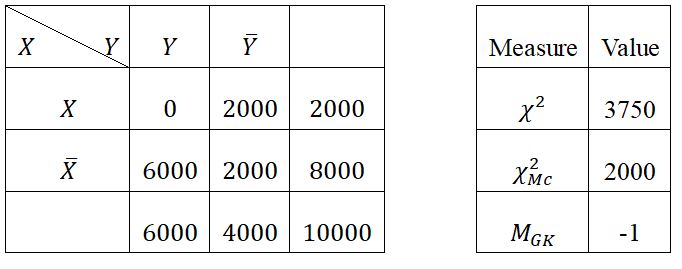
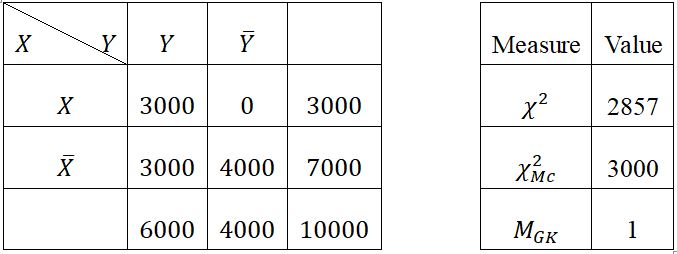
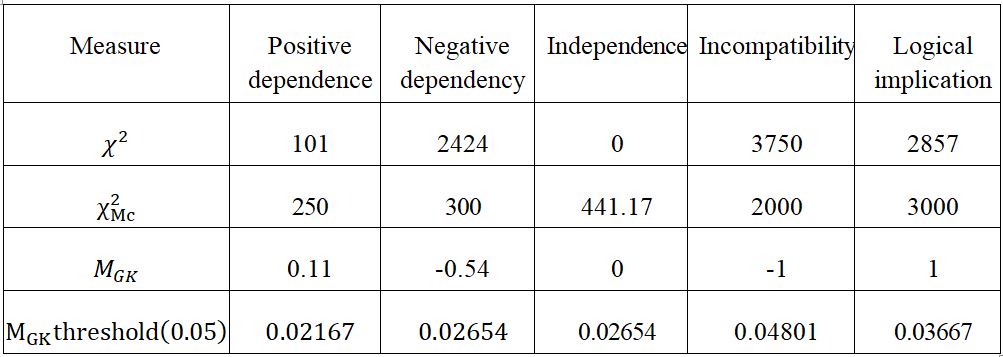
We can see that we don't have the usual relationship, so we will take a few examples already used by Totohasina to compare the Chi-square measure with the measure M_GK in the five reference situations (positive dependence (Table 51), negative dependence (Table 52), independence (Table 53), incompatibility (Table 54) and logical implication (Table 55)) [7].

We notice that at the last table (Table 56), both measures are always positive, belong to the interval , which means that the measurements are symmetrical, i.e. is equivalent to . At independence, the McNemar measure is still positive and different from 0. Compared with its value at negative dependence, we can interpret this as a strong link, since at independence its value is higher than at negative dependence. These facts mean that the Chi-square and McNemar measures are unreliable and fail to meet many of the characteristics of a quality measure of association rules. However, the measure M_GK measures differentiate situations well, moreover its values are only between 0 and 1, differentiated by signs; so can be interpreted as a probability such that the signs only indicate the direction of the link: negative if opposite, i.e. the presence of the other implies the absence of the other, and positive if the same orientation. To sum up, the Chi-square and McNemar measures arse unreliable and very confusing, which is not the case for the measure M_GK.

For a risk α = 0.05, the χ2 (α) with one degree of freedom is equal to 3.841, then:

in positive dependence (Table 5-1), M_GK threshold (0.05) = 0.02654 and M_GK = 0.11 then we accept the implication X→Y (because M_GK ≥ M_GK threshold)

in negative dependence (Table 5-2), M_GK threshold (0.05) = -0.02654 and M_GK = -0.54 , as the both values are negative, and M_GK threshold ≥ M_GK then one of and is valid

• in independence (Table 5-3), M_GK threshold (0.05) = 0.02654 and M_GK = 0 then we cannot say anything

in incompatibility (Table 5-4), M_GK threshold (0.05) = -0.04801 and M_GK = -1, then certainly one of →Y and X→

Conclusion

• in logical implication (Table 5-5) M_GK threshold (0.05) = 0.03667 and M_GK = 1 so we accept without a doubt the implication X→Y

Extracting knowledge from a database is a crucial step in the development of artificial intelligence, since the information is used to make the right decisions. This information includes association rules, which are extracted from a formal database. The quality of an association rule is measured using a probabilistic function, with at least 106 measures listed in the literature. Even if these measures are used to measure the quality of an association rule, their ability to validate rules must also be studied. Therefore, we analyzed and observed the behavior of two measures: the McNemar measure, often used in medicine, and the M_GK. As a result, we found that the McNemar measure is very confusing and indiscriminately validates association rules in the five reference situations, on the one hand. The M_GK measure, on the other hand, distinguishes between cases such as -1 for incompatibility, a value between -1 and 0 for negative dependency, 0 for independence, between 0 and 1 for positive dependency and 1 for logical implication. So, it is best to use the M_GK measure, thanks to its precise filters and reliability.

Conflict of Interest

The authors declare no potential conflict of interests.