Full Text Article

Introduction

In recent decades, photonic crystals [1] have been an active and attractive area in both fundamental and applied research. These artificial structures are composed of dielectric, semiconductor, or metallic materials, with a refractive index that is periodically modulated in one, two, or three dimensions [2]. This periodicity affects the propagation of electromagnetic waves. When light encounters the multilayer structure, certain wavelengths are reflected due to constructive interference, creating a photonic band gap where light cannot propagate. This property makes photonic crystals useful in various applications, such as optical filters [3], reflectors [4], and optical fibers [5].

Physicists have shown considerable interest in one-dimensional photonic systems [6,7] due to their straightforward fabrication and fundamental properties, particularly the emergence of photonic band gaps that inhibit photon propagation for arbitrary polarization in certain or all directions. One-dimensional photonic structures are highly valued for their diverse applications, including reflectors [4], mirrors [8], and optical filters [9], due to their ability to manipulate light by bending, switching, reflecting, and filtering it. The telecommunications sector, in particular, has seen significant technological advancements through the use of photonic fibers [5] based on these structures. Additionally, Fibonacci photonic crystals are especially useful for designing optical filters, given their applications in optical communications. Recently, quasi-periodic photonic crystal [10] structures have gained prominence. These structures can be created using substitution rules involving two building blocks, H and L, with high (nH) and low (nL) refractive indices, respectively. These rules follow aperiodic mathematical sequences such as Cantor [11], Thue-Morse [12], Fibonacci [13], and double period [14]. Fibonacci [13] quasi-periodic photonic crystals exhibit remarkable optical properties that clearly distinguish them from both periodic and random structures. Unlike conventional periodic photonic crystals, which possess well-defined but rigid photonic band gaps, Fibonacci quasi-periodic structures are characterized by their self-similarity and spectral complexity, leading to the formation of multiple and tunable photonic band gaps. This intermediate organization between order and disorder also promotes light localization effects similar to those observed in disordered media, while maintaining coherent propagation. These unique features enable precise control of transmission and reflection over a broad spectral range, paving the way for the design of selective and recon Figureurable optical filters that are highly suitable for telecommunication systems and integrated photonic devices. Despite the extensive research devoted to periodic photonic crystals, studies focusing on Fibonacci quasi-periodic structures remain limited, particularly for Si/SiO₂-based systems [8]. Most previous works have concentrated on high-index contrast materials or purely periodic arrangements, overlooking the potential of quasi-periodicity for fine-tuning optical filtering properties. This lack of detailed investigation into the influence of the Fibonacci sequence and its structural parameters on the spectral behavior of Si/SiO₂ photonic filters represents the research gap addressed in the present study, which aims to demonstrate the ability of such structures to provide tunable, stable, and high-performance optical filters for advanced telecommunication applications. In the present paper, we focus on a Fibonacci multilayer one-dimensional structure using Si/SiO₂ as high/low index materials. This type of structure is investigated theoretically to determine the reflection spectra and optical properties in the infrared range. To optimize these optical properties, we propose a hybrid system composed of periodic and Fibonacci quasi-periodic structures to design optical filters for telecommunications applications.

Theoretical Model

Fibonacci sequence

A one-dimensional Fibonacci [13] multilayer structure is formed by stacking two different dielectric materials: one with a high refractive index (nH) and the other with a low refractive index (nL). The Fibonacci sequence can be constructed by stacking layers according to the substitution rule:

H→L and L→LH.

H et L being two different basic materials representing respectively, the high and the low refractive indexes and I the number of generation of the system.

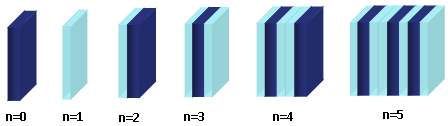
A schematic representation of a Fibonacci multilayers structure with the stacking of H and L materials, for a generation number I varying from 0 to 5, is illustrated in Figure. 1.

H and L denote, respectively, the high and low refractive indexes material.

Periodic Sequence

One-dimensional periodic photonic crystals, also known as Bragg mirrors[8], are structures composed of alternating layers of materials H and L with différent refractive indexes nH and nL which are periodically modulated in one direction.

Matrix Transfer Method

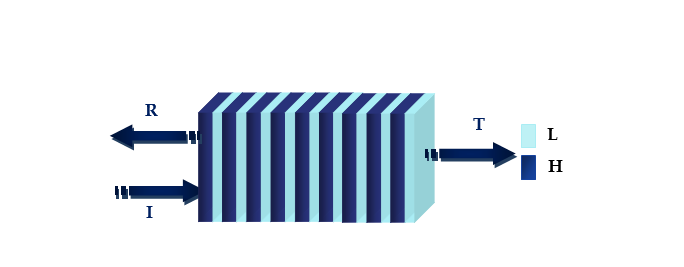
Many methods are used to calculate the reflectance and transmittance in the photonic quasi-periodic one-dimensional structures such as the plane wave expansion method, Fourier transform method, Finite-difference time-domain method and matrix transfer method [6]. In this work, we choose the transfer matrix method which has to study optic properties with a simple theoretical analysis including a clear physical conceptual basis. Matrix transfer method is introduced by yeh which is often used to determine the relation between the amplitudes of incident E₊ (x₀) reflected and transmitted of electric fields after crossing N material layers. It can be related with this relation:

With

The global Transfer Matrix of the multilayer structure

The Transfer matrix of the j^th sequence can be written:

indicates the phase shift of the wave between layers can be obtained by taking

With λ₀ is the reference of the wavelength of the structure, d_j is the thickness of the j^th layer, the complex refractive index and θ_j the complex refractive angle

The Fresnel coefficients t_j and r_j can be expressed

For parallel P-polarization (P)

ForperpendicularS-polarization(S)

The reflectance R is defined by R= |r|²

The transmittance T is defined by

In this numerical investigation, all materials are assumed to be linear, homogeneous, and non-absorbing. We consider waves with normal incidence, resulting in identical reflectance for both polarizations [15]. An iterative algorithm implemented in MATLAB is used to calculate and the reflectance spectra of the quasi-periodic fibonacci structure.

Results and Discussion

Numerical Analysis

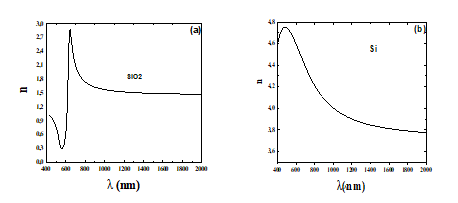
We présented in Figure. 3 the variation of the refractive index n as a function of wavelength of the Si and SiO2 layers deposited.

The variation of the refractive index n with wavelength, shown in Figure. 3, reveals that at longer wavelengths, silicon exhibits a relatively high refractive index (nₛᵢ = 3.4), while silica has a much lower value (nₛᵢO₂ = 1.45). This strong refractive index contrast (Δn = nₛᵢ – nₛᵢO₂ = 1.95) provides a sufficient optical difference between the two materials, which is essential for the formation of photonic bandgap structures. Such a contrast allows light to experience strong reflection and interference effects, leading to the appearance of photonic band gaps that control the propagation of electromagnetic waves.

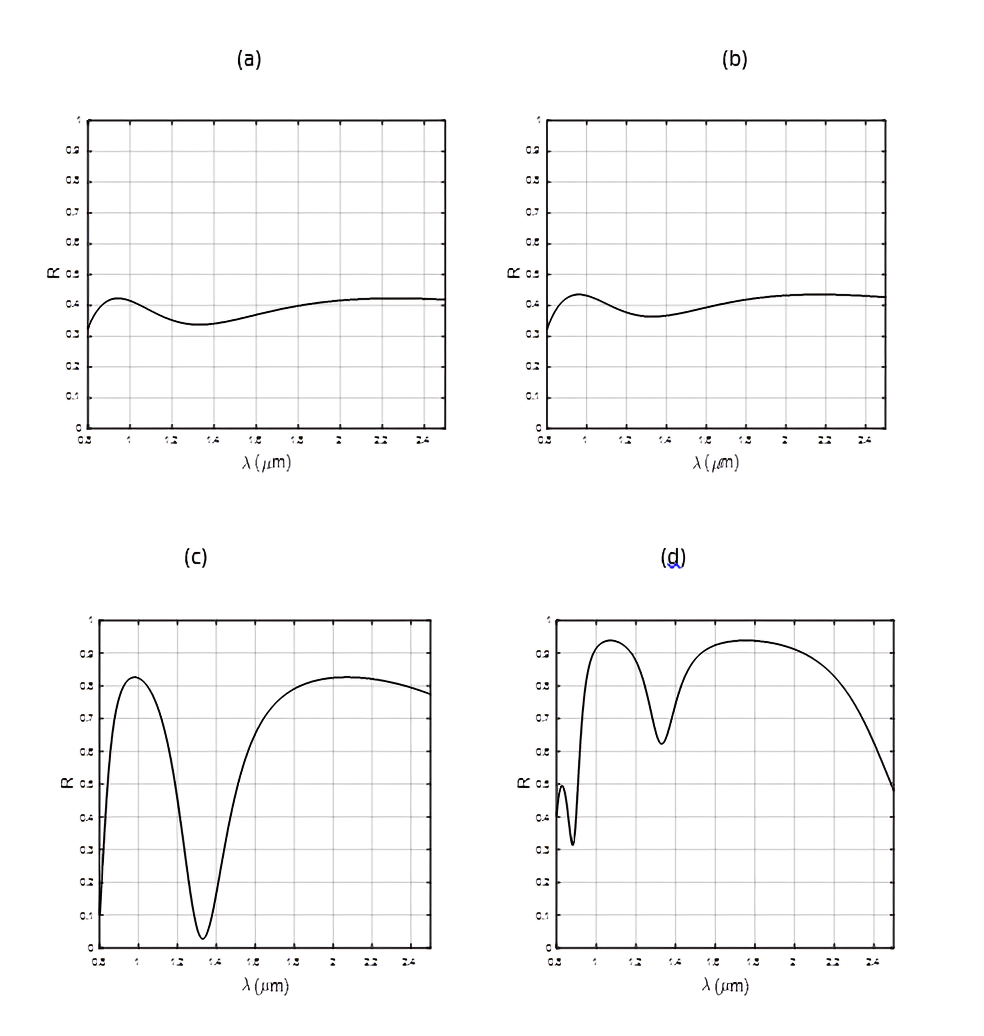
We presented in Figure. 4 the calculated reflectance spectra at normal incidence, obtained using the transfer matrix method for a Fibonacci quasi-periodic one-dimensional photonic crystal. This crystal is based on an arrangement of silica (SiO₂) and silicon (Si) layers, with a low refractive index (nL=1.45) and a high refractive index (nH =3.4), respectively. The thicknesses (d_H) and (d_L) for the SiO₂ (L) and Si (H) layers must satisfy the Bragg condition:

For a reference wavelength λ₀=1.2µm, the thicknesses are approximately 85 nm for the SiO₂ layer and 205 nm for the Si layer.

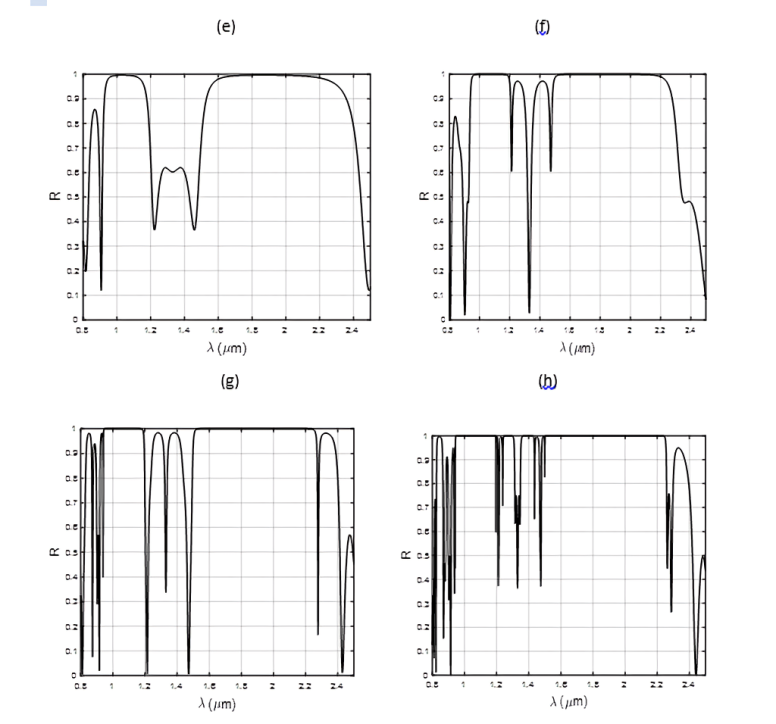
The results obtained in Figure. 4 show that reflectance increases with the number of iterations. We also notice, by analyzing the calculated reflection spectra for different iteration numbers (I= 3, 4, 5, 6, 7, 8, 9, and 10) of the Fibonacci multilayer structure indicated in Figure 3.6, that the photonic band gap (PBG) starts to appear from the 7th iteration corresponding to 13 layers, but this band is not completely defined. By increasing the number of iterations to 8, we observe a PBG that becomes better defined. It is clear that the width of this band remains constant from the 8th iteration and becomes better defined with the increase in the iteration number. This width is determined by calculating the full width at half maximum for the wavelength band corresponding to 100% reflection. Therefore, we can conclude based on this theoretical study that the best performance in terms of the minimum number of layers and the widest band gap is obtained for the Fibonacci distribution structure at the eighth iteration associated with 21 layers at normal incidence. This result is very important since it is possible to experimentally realize this proposed structure due to the ease of depositing such a number of layers [1, 2].

These spectra also show that the PBG is very well defined at the eighth iteration (N=8) corresponding to 21 layers. This band is centered at 1.55µm and extends between 8.39 µm and 2.1 µm with a width of 1.26 µm. This result is interesting because the obtained PBG covers the three telecommunication wavelengths located at 0.85, 1.33, and 1.55 µm. This result can be explained by the choice of deposited materials, which allows us to obtain a good refractive index contrast conducive to the emergence of a wide photonic band gap.

From I=8, the studied reflection spectra clearly show the appearance of three transmission peaks in the PBG at different positions.

The positions of the different transmission peaks obtained from Figure.4 are summarized in Table1.

These effects can be observed in periodic photonic crystals but are due to the introduction of defects in these structures [7-13]. In contrast, in our proposed structure, the transmission peaks appear without the introduction of any defects and are rather due to the choice of the Fibonacci sequence, which allows us to obtain allowed frequency modes. The advantage of this quasi-periodic structure is that it opens localized modes for photons without introducing a new material or even changing the arrangement of these layers. We can therefore affirm that the quasi-periodic arrangement of the layers significantly modifies the optical properties observed in conventional periodic photonic crystals. Quasi-periodic structures thus allow us to localize and propagate light for well-defined wavelengths.

We also notice from the previous reflection spectra that our proposed structure can present several localized frequency modes for the eighth iteration of the sequence. Consequently, the quasi-periodic Fibonacci multilayer system based on Si/SiO2 can be used as a polychromatic filter by varying the number of iterations of the sequence.

From the previous results obtained, we notice that the PBG obtained covers the three wavelengths located at 1.03, 1.085, and 1.444 µm, which correspond to laser diode wavelengths that can be used in several applications as they allow the guiding and propagation of light at well-defined wavelengths.

One of the interesting properties of this structure is its filtering capability, as it allows the selection and separation of wavelengths over very narrow spectral ranges. This makes it possible, for example, to separate the 1085 nm wavelength from the 1.190 µm wavelength, which is crucial for several applications.

Effect of Thickness

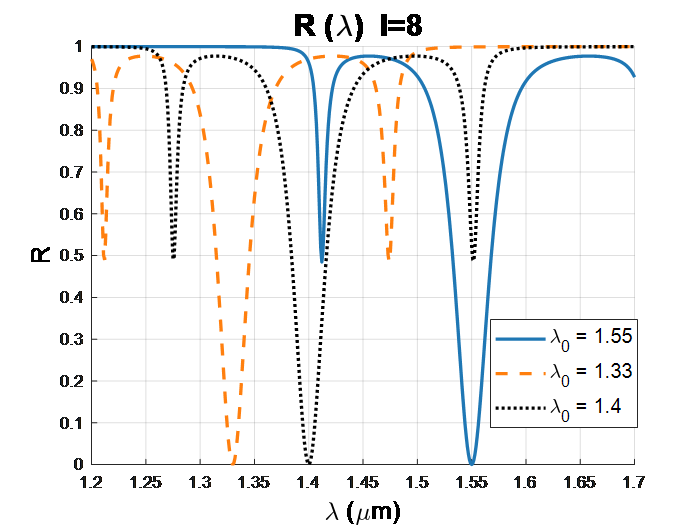
Figure 5 shows the evolution of the width of photonic bands as a function of wavelengths for the eighth iteration (I=8 ) using different thicknesses corresponding to the three reference wavelengths λ₀, which are respectively equal to 1.4, 1.33, and 1.55 µm to satisfy the Bragg condition. We chose these three specific wavelengths 1.33, and 1.55 µm the two corresponding to telecommunication bands and 1.4 µm an intermediate value between them to evaluate the effect of the layer thickness on the position of the transmission peak, while satisfying the Bragg condition.

We notice that the variation in the reference wavelength leads to a shift of the transmission peaks towards longer wavelengths in the quasi-periodic system with a Fibonacci distribution based on Si/SiO2. This shift of the transmission peaks by changing the layer thicknesses allows us to better control and select the filtered wavelengths in our structure according to the For the chosen application, which can enhance the optical performance of the conventional band gap in periodic structures, this improvement broadens the application range of quasi-periodic one-dimensional photonic crystals to include polychromatic filters, demultiplexers, and waveguides.

Optimization of the Optical Filter Properties Based on Fibonacci Photonic Crystal

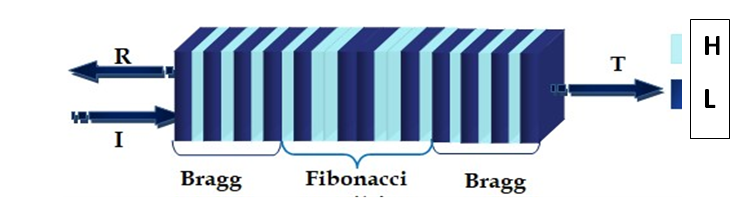
To optimize the optical properties of the filters studied for use in telecommunications, we propose developing a multilayer system that combines two types of structures: periodic and quasi-periodic.

The studied multilayer system consists of two identical Bragg mirrors separated by our Fibonacci multilayer structure, denoted as Brj/FSi/Brj

Where j and i represent the number of iterations of the Bragg structure and the Fibonacci structure, respectively.

The resulting system is shown in the following Figure:

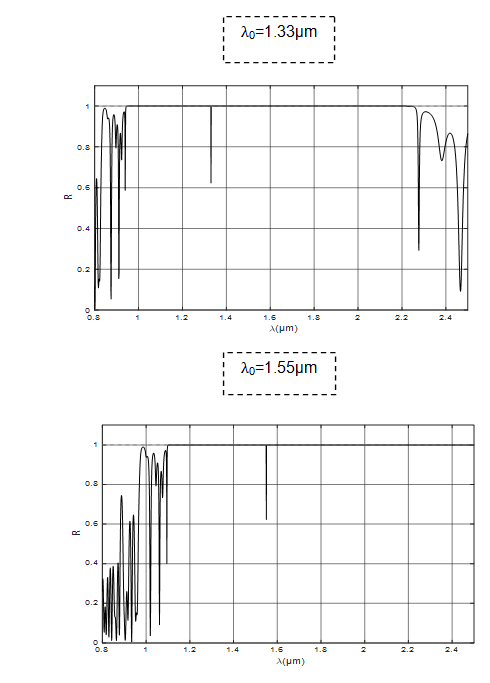
We determined the optimal values of j and i. We set the values of j to 7 and i to 8 to study the optical properties of this system. The following Figurer shows the reflection spectra of the Br (7)/FS (8)/Br (7) system at normal incidence for two different reference wavelengths: 1.33 µm and 1.55 µm:

We observe that the reflection spectra obtained from the hybrid photonic system Br (7)/FS (8)/Br (7) clearly indicate that the photonic band gaps for the two reference wavelengths contain a single localized transmission peak. When using a reference wavelength of 1.33 µm, the transmission peak is located at this same wavelength. By changing the reference wavelength to 1.55 µm, the transmission peak shifts to this new wavelength. We have thus demonstrated that the hybrid multilayer system Br (7)/FS (8)/Br (7) can be used to design monochromatic optical filters. These filters allow for the selection of a single transmission wavelength, either 1.33 µm or 1.55 µm, in the near-infrared range [0.8 - 2.5] µm, by varying the layer thicknesses in our system. The combination of the Fibonacci structure with the periodic Bragg structure enables us to modify the number and position of the transmission peaks, thereby optimizing the optical properties of these filters for telecommunication applications.

Conclusion

In this work, we investigated the optical properties of quasi-periodic photonic structures based on a Fibonacci sequence composed of Si/SiO₂ layers, using the transfer matrix method (TMM) to calculate and analyze their reflection spectra. The obtained results reveal the formation of a well-defined photonic band gap (PBG) in the near-infrared region, which emerges from the eighth Fibonacci generation containing 21 layers and exhibits three distinct transmission peaks. Furthermore, our results show that the Fibonacci quasi-periodic structure presents a significantly broader photonic band gap compared to the conventional periodic Bragg structure. Importantly, this band gap covers the main telecommunication wavelengths (0.85 µm, 1.33 µm, and 1.55 µm), confirming the potential of such systems for use as polychromatic optical filters. To further enhance optical selectivity, we proposed and analyzed a hybrid multilayer conFigureuration combining both periodic and quasi-periodic substructures (Br (7)/FS (8)/Br (7)). The simulated reflection spectra demonstrated that this hybrid design can operate effectively as a monochromatic optical filter for specific telecommunication wavelengths, offering improved control over transmission and reflection properties. This approach thus provides an innovative strategy that merges the advantages of both periodic and quasi-periodic architectures, improving filter performance and spectral tunability. The novelty of this study lies in the introduction of a Fibonacci-based hybrid photonic design and the detailed comparative analysis of its optical response relative to purely periodic structures. Such conFigureurations open promising perspectives for integrated photonics, wavelength division multiplexing (WDM), and optical communication systems, where compact, efficient, and spectrally selective components are required.

For future work, it would be highly relevant to conduct an experimental validation of the proposed models, to investigate fabrication feasibility using current thin-film deposition techniques, and to extend the study to two- and three-dimensional quasi-periodic photonic crystals. These extensions could lead to novel optical functionalities such as omnidirectional reflection, polarization control, and enhanced light localization, further strengthening the potential of Fibonacci-based photonic structures in advanced optical device design.

Conflict of Interest

• The Fibonacci quasi-periodic multilayer photonic structures allow the design of selective optical filters.
• The studied Fibonacci photonic structures are constructed using Si/SiO₂ materials.
• The photonic band gaps of the Fibonacci sequence cover all optical telecom wavelengths (850, 1300, and 1550 nm) in the near-infrared range.
• The positions and number of transmission peaks in the photonic band gaps depend on the parameters of the Fibonacci sequence.
• Using hybrid photonic structures allows for the optimization of the optical properties of the selective filters.