Full Text Article

Introduction

Discovery of carbon nanotubes in 1991 and the subsequent determination of their remarkable electronic properties aroused interest on the silicon and germanium nanotubes and nanowires [1-16]. Since the silicon and germanium played an extremely important role in microelectronic devices, it is expected that the one-dimensional Si and Ge nanostructures are to be of great practical importance in nanoelectronics. The study of silicon-germanium nanotubes and nanowires is also of great interest, because the composite silicon-germanium materials can combine and enhance some of the advantages of their individual components [17-20]. In the last decade, the structure, stability, and electronic properties of SiGe nanotubes were studied using the quantum chemical ab initio tight-binding calculations and classical molecular dynamics [21-28]. An important information on the band structure of SiGe nanotubes was obtained in the previous ab initio calculations and qualitative models, however, all these calculations were carried out using the non-relativistic approaches neglecting the spin-orbit interaction, but spintronics on nanomaterials is currently rapidly developing. It is a field of research closely related to the transfer of electron spins and creation of spins currents in materials in which spin-orbit effects play surely a primary role [29-35]. Note also that the previous tight binding calculations of the SiGe nanotubes were performed with account of a translational symmetry only, but neglecting their helical and rotational symmetries. Taking into account all the symmetry properties of a material is necessary for a more complete and accurate description of its electronic structure. This is absolutely necessary for the calculation of chiral compounds with huge translation cells.

The purpose of this work is a theoretical study of the electronic and spin states in SiGe nanotubes in the terms of a symmetrized relativistic linear augmented cylindrical waves method (LACW). Using the LACW technique, in previous works we calculated the electronic and spin properties of carbon, silicon, gold and platinum nanotubes, including the chiral ones [36-39]. Calculations of the spin properties of chiral compounds are of particular interest because the chiral spin currents are formed in chiral systems, when the spins moving in the material are also chiral, which is used for spins filtering, chirality-induced spin selectivity of the electrical and optical properties of the materials, in the spin-dependent transfer of information [30-33].

Method of Calculations

In the LACW method we apply a two-component relativistic Hamiltonian written using Rydberg units

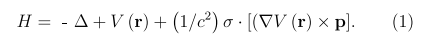
The first two terms describe the non-relativistic H part of the Hamiltonian, and the last term represents the contribution of the spin-orbit coupling, H_S-O here c, σ, and p are the speed of light, Pauli matrix, and electron momentum, respectively. For a potential V(r), we apply the Slater muffin-tin and the ρ^1/3approximations usually used in a standard linearized augmented plane waves (LAPW) theory [40-42], the LACW method being an extension of the LAPW approach to the systems with the new (cylindrical) geometry and new boundary conditions. When constructing the Hamiltonian and basis functions, we take into account all the symmetry properties of nanotubes and reduce the unit cells of any SiGe nanotube to the two neighboring Si and Ge atoms [23]. At the first stage, the eigenfunctions Ψ_λ0and eigen energies E_λ0of the non-relativistic part of the Hamiltonian are calculated. Then the basis is doubled by including the spin functions Ψ_λ0χ (where χ = α or β are spin functions for electrons with spins up and down) and the H_S-O matrix elements in the spin-dependent basis set are calculated. Explicit formulas for the basis functions and secular equations for the non-relativistic and relativistic versions of the LACW method are given in the original papers and in the recent monograph [43-45]. Finally, the energies and wave functions of the Hamiltonian (1) are determined by diagonalization of a secular equation.

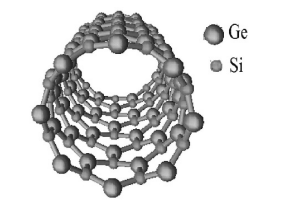
In order to calculate the SiGe nanotubes, one has to specify their geometry. The SiGe nanotubes have the form of cylindrical surfaces covered with Si₃Ge₃ hexagons (Figure 1) with interatomic distances d_Si-G= 2.37 Å [23]. They can differ in diameter, orientation of hexagons relative to the tube axis, and, finally, chirality, when one enantiomer has a right-handed and the other a left-handed helical axis. The orientation of hexagonal cells relative to the tubule axis is usually described by two integers (n₁ , n₂ ), where n₁ > 0 and 0 ≤ n₂ ≤ n₁ . The nanotubes (n₁ , n₂ ) have a rotational symmetry axis Cn , where n is the greatest common divisor of the n₁ and n₂ indices, and a screw S(h, ω) symmetry in the form of repeated shift operations by

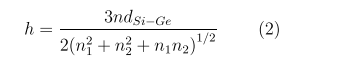
along the z-axis of the cylinder with simultaneous rotation through an angle

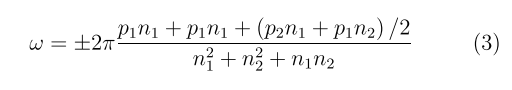
around this axis. Positive and negative signs of ω for chiral nanotubes correspond to tubes with positive (right-handed) and negative (left-handed) helicity; the integers p₁ and p₂ are to be found from the equation p₂n₁ − p₁n₂ = n). The previous calculations of the SiGe nanotubes geometry show that they have a weakly corrugated structure, when the radii of the cylindrical surfaces formed by Si and Ge atoms differ by ΔR ≈ 0.3 Å so that the Ge atoms are slightly displaced inside the cylindrical layer, and the Si atoms outward [23].

As the typical examples, we discuss below the calculations of two non-chiral SiGe nanotubes (7,7) and (12,12) with “armchair” and “zigzag” geometries, and of the three chiral systems SiGe (10,4), (9,6) and (11,3). These nanotubes have similar radii of 7.5-8.5 Å, but sharply different chirality angles α

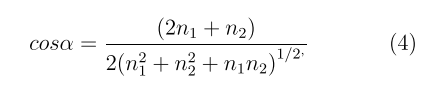
where the values of α lie in the interval 0 ≤ α ≤ 30°, with α = 0 and 30° corresponding to non-chiral tubes (n,n) and (n,0), and other α values, to the chiral tubes with helical geometry.

Results and Discussion

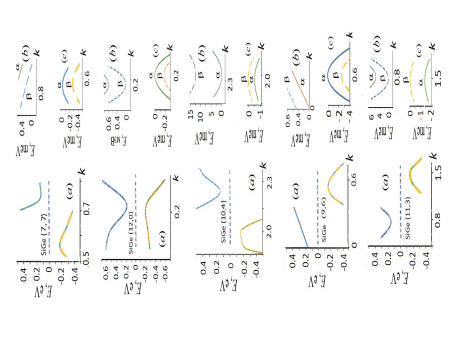
Figure 2 shows the band structures of the five SiGe nanotubes presented using the repeated zone scheme, according to which the eigenstates of the compounds depend on the wave vector ‒π/h ≤ k ≤ π/h and on the rotational quantum number 0 ≤ L ≤ n ‒ L [43-45]. Note that in this figure the results are given for positive values of k only, since neglecting the spin-orbit gaps indistinguishable at this energy scale, the dispersion curves are symmetrical with respect to the sign change of the wave vector E(‒k) = E(k). Taking into account all the symmetry properties of nanotubes and reducing the unit cell to two atoms with eight valence electrons allows to present the electronic structure of compounds in the form of four doubly filled dispersion curves of the valence band separated by an optical gap from the conduction band. In all cases, the width of the valence band is about 12 eV and includes an internal band of predominantly s electrons of Si and Ge atoms with a width of 2 eV and an upper band of three dispersion curves of p electrons with a width of about 8 eV. In agreement with previous tight-binding calculations [23], all tubules regardless of geometry have the semiconducting band structure with the band gap E_gequal to about 0.35 eV (Table 1). This is a significant difference between SiGe nanotubes and carbon or silicon analogues having the semiconducting, semimetallic or metallic properties depending on geometry. The difference is due to the polarity of the Si-Ge chemical bonds and, as a consequence, the effect of the antisymmetric component of the electronic potential leading to the repulsion of symmetric bonding and antisymmetric antibonding occupied and vacant electronic states. Stability of the E_g values with respect to variations in the structure of tubules can be useful from the point of view of their applications in nanoelectronics, since it should facilitate production of the semiconducting nanotubes with reliably reproducible characteristics.

Figure 3 shows on an enlarged scale the effects of spin-orbit splitting of levels located near the edges of the valence and conduction bands for the non-chiral and righthanded chiral SiGe nanotubes and positive values of the wave vector k. For the k > 0, spin up (α) corresponds to the case when the chirality, electron flow, and spin vectors are oriented parallel in the direction z > 0, and spin down (β), when it is oriented in the direction z < 0, that is opposite the chirality and electron flow vectors. For the negative k values, the corresponding dispersion curves are obtained from this figure as follows. By Kramer’s theorem, for systems that do not have inverse symmetry such as the chiral tubules, when the sign of k changes, the electron energy remains the same, but the spin polarization changes to the opposite

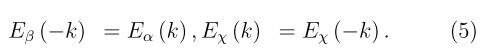
For the non-chiral tubules, due to the additional (inverse) symmetry, both the energy and spin polarization are conserved

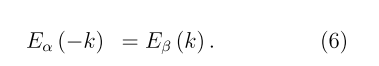
Consequently, the spin-orbit interaction manifests itself differently in nanotubes of different helicities. For example, in the non-chiral nanotubes (7,7) and (12,0), the minimum energy gap corresponds to the α→β transition between the valence and conduction bands at the relevant positive and negative k values (e.g., at |k| ≈ ± 0.2 a.u. for (12,0) tubule). As a result of the Eq. (5), the transfer of α electrons located in the region of the top of the valence band should coincide in the directions z > 0 and z < 0. The same should be true for the β electrons of the bottom of the conduction band of these non-chiral nanotubes.

For chiral nanotubes, the Egs. (5) determine the dependence of the direction of electron flow along the tubule axis on the orientation of their spins. As an example, let us consider a right-handed nanotube (9.6). At k > 0, the top of the valence band and the bottom of the conduction band are formed by electrons with spin α, so the transfer of electrons with this spin will dominate in the direction z > 0 under the influence of an electric voltage U of the corresponding sign. According to the Eqs. (5), at k < 0, the boundary states of the bands are to be formed by electrons with β spins. If we now change the sign of the voltage U to ‒U and thereby reverse the direction of the electron flow, then the transfer of electrons with β spins in the ‒z direction will predominate. This effect is due to the difference in the mobility of alpha and beta electrons in the direction of the helical axis and against it. It is an example of so-called chirality-induced spin selectivity, which has become the focus of research in recent years discussed in detail in the works [29-36]. For right-handed (11,3) nanotubes, the minimum electron excitation energy corresponds β → β transition without flipping electronic spin, and with the help of this tubule it is possible to realize the preferential transport of β electrons in the positive direction of the axis and of α electrons in the opposite direction. In the right-handed nanotube (10,4) with the β → α minimum gap, the positive direction of transfer is favorable for electrons with spin β at the top of the valence band and electrons with spin α at the bottom of the conduction band

The energies of the spin-orbit gaps E_v,SO and E_c,SO of the valence band and conduction band edges differ markedly for non-chiral and chiral nanotubes. In the first case, the E_v,SO and E_c,SO are several tenths meV, in the second several meV, maximum E_c,SO = 12.8 meV for the tube (10.4) (Table 2). Using a mechanical effect on a nanotube, for example, by twisting it around a cylindrical axis in a positive or negative direction, stretching or compressing it along the axis, one can change the energies of the spin-orbit gaps, which is important for controlling of spin transport in tubes and for creating the devices for nano-spintronics and nano-electromechanics. In non-chiral nanotubes (7,7) and (12,12), torsional deformation is a low-symmetry perturbation, the magnitude of which does not depend on the sign of deformation. The calculations show that the torsional deformation by an angle of 1°/Å in a positive or negative direction causes an increase in the gaps E_v,SO and E_c,SOin tubes (7,7) and (12,0) by a maximum of 1 meV. A response of the spinorbit gaps of chiral tubes obviously depends on the sign of the deformation and is stronger, as can be seen from numerical calculations. The maximum response to torsional deformations is a decrease in E_c,SO by 7 meV for the (10,4) tube when it is twisted at an angle Δω = 1°/Å in the direction of the chirality of the right-handed helical system and an increase in E_v,SO from 0.33 to 14.76 meV at twisting the tube (9,6) in the opposite direction at an angle Δω = ‒1°/Å. Axial deformations do not change the chirality of nanotubes and have a weaker perturbation of the spin states of the band edges compared to the effects of torsional deformations. Typical variations in the energy of the spin gaps of the band edges when the length of the nanotubes changes by ±1% lie within 1 meV.

Finally, we note that diagrams shown in Fig. 3 for right-handed chiral nanotubes are easily transformed into band structures of tubes with left-handed helicity. To do this, it is enough to change the directions of the spins α and β of the dispersion curves,

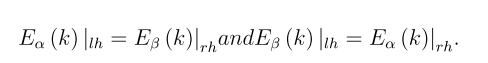
Conclusion

Single-walled silicon-germanium nanotubes are semiconductors with minimum optical gaps almost independent of the chirality of the tubules. The spin-orbit splittings of the valence and conduction band edges are several tenths of meV in non-chiral nanotubes and can exceed 10 meV in chiral materials. The energies of spin-orbit gaps and the spin properties of nanotubes are strongly sensitive to the torsional and axial deformations, which can be used to control spin transport in nanotubes.

Financing the Work

The study was supported by the Russian Science Foundation, Grant No. 22-23-00154, https: rscf.ru/project/22-23-00154/

Author Declarations

Conflict of Interest

The author has no conflicts to disclose.

Data Availability

The data that support the findings of this study are available within the article.