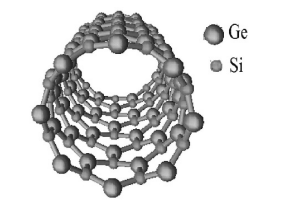
Figure 1: Typical structure of the SiGe nanotube
Nanotube |
RNT, Å |
Chirality angle, α° |
Eg, eV |
(7,7) |
7.65 |
30 |
0.35 |
(12,0) |
7.60 |
0 |
0.38 |
(10,4) |
7.87 |
16 |
0.37 |
(9,6) |
8.53 |
23 |
0.37 |
(11,3) |
8.32 |
12 |
0.34 |
Table 1: Geometric parameters RNT and a and band gaps of SiGe nanotubes for h and ω values calculated using Eqs. (2) and (3)
Geometry |
Ev,SO, meV |
Ec,SO, meV |
(7,7) |
||
ω, h |
0.13 |
0.02 |
+Δω |
0.50 |
0.97 |
‒Δω |
0.50 |
0.97 |
+Δh |
0.45 |
0.89 |
‒Δh |
0.24 |
0.82 |
(12,0) |
||
ω, h |
0.18 |
0.57 |
+Δω |
0.14 |
1.26 |
‒Δω |
0.14 |
1.26 |
+Δh |
0.22 |
0.53 |
‒Δh |
0.20 |
0.60 |
(10,4) |
||
ω, h |
0.63 |
12.81 |
+Δω |
0.98 |
5.59 |
‒Δω |
1.91 |
6.07 |
+Δh |
0.41 |
12.46 |
‒Δh |
0.46 |
11.37 |
(9,6) |
||
ω, h |
0.33 |
0.44 |
+Δω |
5.38 |
0.24 |
‒Δω |
14.76 |
0.38 |
+Δh |
1.78 |
0.59 |
‒Δh |
0.48 |
0.75 |
(11,3) |
||
ω, h |
1.45 |
4.76 |
+Δω |
1.11 |
3.04 |
‒Δω |
1.70 |
4.43 |
+Δh |
1.11 |
5.80 |
‒Δh |
1.54 |
4.86 |
Table 2: Energies of spin-orbit splittings of the of valence band Ev,SO and conduction band Ec,SO edges for the equilibrium geometry of nano- tubes with h and ω values calculated using Eqs. (2) and (3), as well as for nanotubes subjected to the torsional deformations at angles △ω =±1°/Å in the positive or negative directions, and stretching or compressing deformations along the z axis by 1% (△h = ±0.01h)

Figure 1: Typical structure of the SiGe nanotube

Figure 2: Band structures of SiGe nanotubes (7,7), (12,0), (10,4), (9,6), and (11,3). The values of the wave vector k at the Brillouin zone boun- daries k = π/h are equal to 0.818, 0.461, 2.92, 2.04 and 5.98 a.u., respectively. Arrows show the positions of conduction and valence bands edges
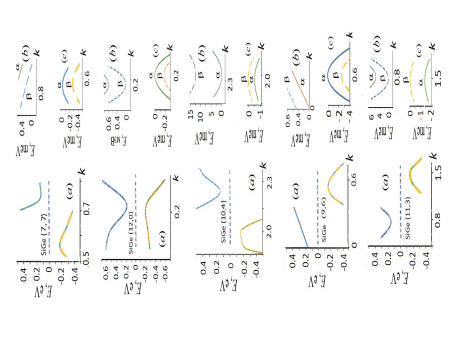
Figure 3: Spin-dependent electronic levels of nanotubes in the regions of valence and conduction band edges. General view (a), bottom of the conduction band (b), and top of the valence band (c). For chiral nanotubes, the diagrams shown correspond to tubules of right-handed helicity
Tables at a glance
Figures at a glance