Full Text Article

Introduction

Motivation for Data-Driven Materials Discovery and Optimization

The study of materials science and engineering has been generally regarded as a pursuit toward the understanding of the relationships among materials processing, structure, properties, and performance. Within these characteristics lie endless possibilities—synthesis, fabrication, and characterization techniques are numerous and varied, and the creation of a material can involve a multitude of techniques. Furthermore, these methods can be performed at any number of specified conditions, introducing an even high dimensionality to this materials parameter space. Essentially, the number of potential materials and the paths to their optimization are virtually infinite. This vast continuum of choices presents both opportunities and obstacles to researchers. While the enormity of materials parameter space endows the discipline with robust and diverse research topics, it also presents the challenge of thoroughly exploring the unlimited extent of potential materials. The increasing rapidity of advances in materials synthesis and processing therefore necessitate the development of intelligent, data-intensive methods for materials discovery and optimization.

Conventional Computational Methods in Materials Science and their Limitations

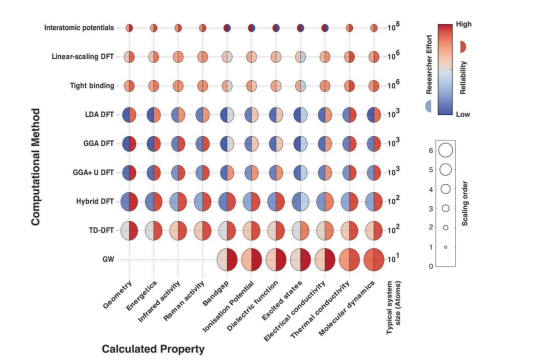
Conventionally, first-principles computational methods have employed for material design and optimization. Variants of density functional theory (DFT), tightbinding methods, and many bodied GW approaches have been used extensively to understand and improve materials properties ranging from band gaps to molecular dynamics. In a 2016 article in Chemical Society Reviews, Butler et al. [1] analyzed the computational expense and reliability of computational methods in materials science and created the schematic shown in Figure 1. In this image, the shade of the left semicircle corresponds to the difficulty of the method for the researcher, the shade of the right semicircle corresponds to the reliability of the method, and the scale of the circle represents the scaling of the computational effort with system size.

The Figure 1 graph demonstrates the classic tradeoff between the accuracy of a computational method and its cost, factoring in the additional opportunity cost of a researcher’s time and expertise. Most computational researchers tend to choose a DFT variation-these techniques typically have a relatively high reliability and a relatively low researcher effort, as shown by the generally blue tones in the left halves of the DFT circles and the generally red tones in the respective right halves.

While these traditional computational methods have successfully addressed countless materials science research questions, they do suffer from certain limitations. In 2008, Cohen et al. provided insights into the current limitations of DFT in a powerful article in Science [2]. Cohen identifies the exchange-correlational functional as the key component that determines the ultimate success or failure of a DFT simulation. Significant complications in the exchange-- correlational functional arise from the extension of the Pauli Exclusion Principle to a many-bodied system. The Pauli Exclusion Principle states that the wave function for two identical fermions is antisymmetric with respect to the exchange of the two particles. This implies that the wave function will switch signs if both the space and spin coordinates of the identical particles are swapped. The exchange correlation functional describes the many-body interactions that occur as a result of this antisymmetric relation. However, the exact form of the exchange-correlation in terms of density is not precisely known, and approximations must be used. While simple approximations have performed particularly well for the prediction of the structure and thermodynamic properties of materials, errors in the approximations for complex exchange-correlation functionals account for substantial failure in the prediction of properties. These challenges have caused simulations to underestimate band gaps, energetic barriers to chemical reactions, and charge transfer excitation energies, among others. In addition, DFT struggles to adequately model systems with many degenerate states, such as in transition metals, highly correlated systems, or the breaking of atomic bonds.

These difficulties in approximating the exchange-- correlation functional embody a fundamental limitation of atomistic, ab initio approaches. Since these methods derive results from the current understanding of quantum mechanics, they naturally lack methodology for adequately incorporating any presently unexplained mechanisms into mathematical models. Conversely, recent advances in machine learning provide approaches for pattern recognition and prediction from data a priori. In essence, the implementation of machine learning methods can provide predictions from data despite scarce information about specific underlying mechanisms. While traditional ab initio approaches are a core tenet of computational materials research, modern methods in machine learning demonstrate the potential to overcome conventional computational barriers and to address applied problems where ab initio approaches may not be applicable.

Machine Learning in Science and Engineering

Machine learning is a discipline centered on the study of algorithms that can learn from and make predictions about data based on sample input data, rather than explicitly defined relationships. While machine learning has been a prolific research topic in computer science and mathematics for over half a century, these methods have also become a cornerstone in fields such as genomics [3], biological image analysis [3], and drug design [4] within the past several decades. In computational biology, groups such as Xiong et al. have used deep neural networks to predict gene splicing activity and genetic determinants of disease [5]. Additionally, convolutional neural networks are widely used method in biological image analysis; Ning et al. successfully predicted abnormal development from embryo images [6], and Xu et al. classified colon histopathology images as cancerous and non-cancerous [7]. Machine learning techniques have been used in essentially all facets of drug design research-Cong et al. used a genetic algorithm-based model to predict the activity of H1N1 influenza inhibitors [8], and Wang et al. used convolutional neural networks to develop a highly-accurate computational for the prediction of protein secondary structure [9]. Applications of neural networks and other forms of machine learning are now essentially commonplace in these research areas.

As disciplines, computational biology and materials science are similar in their focus on understanding relationships between molecular or atomic structure and the resulting properties. Therefore, it is relatively surprising that the application of machine learning techniques to materials science has been comparably slow; these methods are not yet conventional in materials science, yet there are countless machine learning frameworks for the analysis of genomic sequences, cross-disciplinary image analysis, and drug development. In a recent review of evolutionary algorithms in materials research, Le and Winkler [10] partially attribute the lack of machine learning in materials science to relevant articles being published in mainly computer science journals. This justification seems dubious, based on both the rigorous application of machine learning to computational biology and the interdisciplinary nature of materials science. Rather, it is more likely that the relatively recent advances in high throughput synthesis and characterization methods now present machine learning techniques as increasingly viable methods for data analysis. This explanation is particularly probable considering the history of machine learning in computational biology; the role of machine learning in genomic research has always necessitated a massive amount of sequencing data, which became increasingly available with improvements in high-throughput sequencing methods over the last few decades.

Furthermore, big data collaboration and open source databases have become increasingly popular in the general scientific community in the past decade, perhaps leading to a renewed interest in developing materials databases and adopting machine learning techniques for materials research. Individual research groups and university organizations alike have begun developing their own materials data repositories. A creation of the Wolverton lab at Northwestern University, the Open Quantum Materials Database (OQMD) offers over 400,000 DFT-calculated thermodynamic and structural properties of materials [12]. On a larger scale, the NanoHub organization at Purdue University has introduced the Nanomaterial Registry [13]. This provides a wealth of information about nanomaterial’s, including details about the preparation and synthesis of samples and links to publications and relevant environmental studies. The expansive development of materials databases demonstrates an escalating interest in an informatics-driven approach to materials design and optimization. However, with these databases still in their relative infancy, there is minimal regulation of data quality or structure, resulting in concerns about the reliability and practicality of data sets.

With the introduction of the Materials Genome Initiative (MGI) by President Obama in 2011, the opportunity for materials data collaboration and standardization has dramatically improved [14]. This initiative represents the collaboration of federal agencies, national labs, and the private sector to develop policy, resources, and infrastructure for the discovery and production of advanced materials. Institutions spanning the Department of Defense (DoD), the National Science Foundation (NSF), the National Renewable Energy Laboratory (NREL), and the National Aeronautics and Space Administration (NASA) have collectively contributed over half a billion dollars in the pursuit of advanced materials. A significant component of this pursuit is the push toward making relevant digital data accessible. The National Institute of Standards and Technology (NIST) created the Materials Data Repository (MDR), which allows public access to over 50 gigabytes of heterogeneous material data and any corresponding metadata. As an MGI collaborator, the DOE has also established multiple computational databases and tools. Initiated by the DOE, the Materials Project at the University of California, Berkeley, uses innovative theoretical tools to identify and predict influential clean energy materials. Additionally, the DOE founded the Center for Predictive Integrated Structural Materials Science (PRISMS), which combines experiments, theory, and simulation into unique computational tools for predicting structural materials. The integration of diverse areas of materials research embodies a second tenet of the initiative: an effort to shift the paradigm approach to materials research by blurring the conventional lines between experimental and computational work.

Since its inception in 2014, the MGI has catalyzed efforts to accelerate the discovery, design, and development of new materials through the integration of computational tools and data with experimental work. As one notable early success, the MGI infrastructure supported the development of a new formulation for the U.S. Mint’s new five-cent coin. Given the increasing market cost of nickel, the U.S. Mint sought a new formulation of the coinage material with certain specifications. The MGI data and computational tools enabled NIST to design a new coinage material that met the required parameters within 18 months, whereas traditional methods usually necessitate three to five years [15]. The number of institutions leveraging MGI data and tools continues to grow-the organization’s Fifth Principal Investigator Meeting in June 2022 highlighted work from dozens of research groups experimenting with emerging machine learning approaches and cross-cutting research strategies to advance materials discovery and optimization. One research group, with a project entitled “Design and Synthesis of Novel Magnetic Materials,” stated that their work has led to the development of a comprehensive magnetic materials database. Leveraging this database, the group uses an adaptive genetic algorithm coupled to first-principles codes to predict properties of potential magnetic materials. As a result of these efforts, the researchers are exploring a patent for materials related to their work on Fe-Co-B compounds, which were predicted by machine learning techniques and synthesized by experiment. Numerous other institutions report the pursuit of patents, contributions toward open-access materials data, and educational activities to support the development of the next generation of materials science workforce [16]. As another marker of MGI’s success, the MGI Strategic Plan indicates that usership of the MGI materials information infrastructure has grown exponentially, from less than 10,000 users in 2014 to over 150,000 users in recent years [17]. These early achievements demonstrate the growing potential of the MGI, as it strives toward its goals to create a unified materials innovation infrastructure, harness the power of materials data, and train the research and development workforce. Despite increasing momentum to improve the availability and accessibility of materials data, the application of machine learning techniques to materials science problems may face a secondary challenge. Materials science, with its roots in physics and chemistry, has always pursued an understanding of the relationships among materials processing, structure, properties, and performance; methodology for improving materials sans the understanding of an underlying mechanism is unconventional. It’s possible that therein lies another reason why materials scientists have been slow to embrace machine learning-the “black box” nature of certain algorithms does not enable researchers to uncover the reasoning behind materials optimization.

Accordingly, researchers may be concerned about the foundations and the legitimacy of these methods; for example, there are review articles regarding how machine learning methods, specifically neural networks, have been incorrectly applied in materials science [18,19]. These articles note issues with small sample sizes or the choice of algorithms that are not ideal, or even suitable, for a particular problem. Since neural networks are used as predictive models, these issues are certainly concerning; the development of an incorrect model would lead to inaccurate predictions. However, this isn’t the case with optimization algorithms; in this instance, the use of too small a sample size would lead to a limited exploration of parameter space. This would result in a globally suboptimal choice for the material, but the material would still have improved properties. Thus, in the realistic context of a search for an improved (though not necessarily optimal) material, optimization algorithms have an inherent degree of flexibility in their methodology. Researchers appear to be navigating these challenges by adeptly pairing machine learning models with other firstprinciples computational research, to preserve the ability to investigate fundamental, underlying mechanisms while advancing optimization processes [16].

Machine Learning in Materials Science: Evolutionary Algorithms

Of the machine learning techniques that have been utilized in materials research, evolutionary algorithms remain some of the most extensively used. During the mid-1960s and early 1970s, several research groups began independently developing evolutionary algorithms. Researchers in the USA established simple genetic algorithms (SGAs) and evolutionary programming (EP), while scientists in Germany developed evolution strategy (ES) [20]. Later developed methods include particle swarm, genetic swarm, and ant colony optimization. These approaches vary in their methodology, but they all apply biological principles to non-biological optimization problems. Drawing from evolutionary concepts such as reproduction, replication, and mutation, evolutionary algorithms use concepts inspired by natural selection to methodically determine the ideal characteristics for a system. In general, evolutionary algorithms involve initializing a population, evaluating the quality of the members, altering that population using evolutionary operators, and repeating until the quality of members have exceeded a certain threshold.

In the context of materials science, evolutionary algorithms evolve a population of materials toward an improved property by determining an optimized set of characteristics for that material. While materials researchers have predominantly used variations of simple genetic algorithms to approach optimization problems, other evolutionary algorithms are not without representation. In 2011, Giaquinto et al. used particle swarm optimization to determine homogeneous upconversion coefficients in Er³⁺ -doped glasses and erbium-activated devices, demonstrating an alternate method for determining these parameters without the expensive equipment typically used to measure them [21]. Additionally, ant colony optimization has been used as a method to find the lowest energy configuration of silicon atomic clusters [22]. Nonetheless, genetic algorithms remain the most common choice for researchers applying evolutionary approaches to their research.

While evolutionary algorithms are one application of machine learning techniques, numerous other algorithms and approaches are common and emerging in the field, and the present state of machine learning algorithms for materials science is well-described in the literature. As one example, Chong, et al. provides an overview of machine learning algorithms used in materials science, in a review article for Frontiers of Physics. The article enumerates common machine learning methods, including kernel-based linear algorithms, neural networks, decision tree and ensembles, unsupervised clustering, generative models, and transfer learning, as well as emerging machine learning models, including explainable artificial intelligence methods and few-shot learning [23]. While many other machine learning techniques beyond genetic and evolutionary algorithms are effectively employed in the field, the scope of this work will be to detail and comment on the broad application of genetic algorithms to materials science and engineering. Genetic algorithms present several advantages that support effective discovery and optimization, which is particularly of interest for materials science researchers-particularly, these algorithms are adept at optimizing among large parameter spaces, and they are well-suited to solving problems in nonlinear or multimodal parameter spaces. Genetic algorithms, therefore, are one tool that can be integrated into materials research, and recent work in the field demonstrates the pairing of genetic algorithms with other computational techniques to facilitate materials discovery and optimization.

Accordingly, the remainder of this article will address the mechanics of genetic algorithms and case studies specific to materials optimization and discovery. In Section 2, the typical mechanics and methodology of genetic algorithms are presented, and their implementation in materials research is broadly described. Then, Section 3 focuses on a single field of application: the optimization and discovery of inorganic phosphors with genetic algorithm-assisted methods. This case study serves to exemplify the challenges involved in combining experimental and computational approaches, as well as to demonstrate the relevant subfields in which genetic algorithms may be applicable. In this final section, some mention will be given to the myriad applications of genetic algorithms in materials science, but these are well-detailed elsewhere. Rather, this work aims to present commentary on the efficacy of the application of genetic algorithms to materials science problems, and to discuss the future role of machine learning in materials research and development.

Genetic Algorithms

Overview of Genetic Algorithms

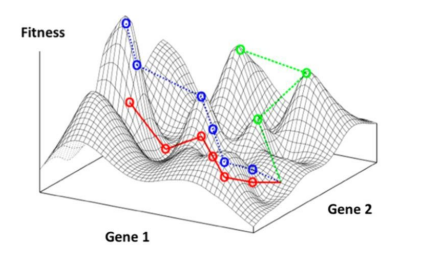
Fundamentally, genetic algorithms are metaheuristic optimization methods: they generate approximate solutions in parameter spaces that are too large to be comprehensively explored [10]. Genetic algorithms are especially suited to address materials discovery and enhancement due to their optimization-based design and their capability of handling high-dimensional parameter spaces [20]. As noted in the previous section, genetic algorithms draw upon concepts from natural selection, such as reproduction, inheritance, and mutation. However, in the case of materials engineering, the evolving population is a set of diverse materials. Each individual material is a member of the population, and it is characterized by a selected set of properties. These chosen attributes are represented mathematically, and they are known individually as the genes of the member, or comprehensively as a genome of the member. Based on the member’s genes, a given material’s genome has an associated fitness, determined by a fitness function. The fitness of a member is essentially a score that represents how well the particular genome optimizes the desired property or set of properties. The fitness function is the specific function that maps the mathematical representation of the genes to the fitness. Since each material’s genome has an associated fitness, the population of all possible materials genomes has an associated fitness landscape, as demonstrated in Figure 2. The objective of implementing a genetic algorithm is to identify the material genome that has the greatest fitness, thereby optimizing the desired characteristics of the material.

A successful navigation of the fitness landscape is dependent on two assumptions: (1) the genomes in consideration are numerous and varied enough to adequately represent the essential features of the fitness landscape, and (2) the properties associated with the fitness are well-defined for the chosen genomes [10]. With regards to the first assumption, consider a fitness landscape with multiple local maxima, as shown in Figure 2. It is evident that different optimization paths may yield different results for the optimal genome. For example, the dotted blue path leads to the true maximum, associated with a genome that has certain values for Gene 1 and Gene 2. Conversely, the dashed green path and the red line path lead to suboptimal fitness values, and the dashed green path results in a material with a starkly different genome. While finding local maxima for the fitness will still improve the resulting properties, it is undoubtedly ideal to seek a global maximum. As such, it is essential to consider a representative variety of genomes that will provide a thorough understanding of the fitness landscape. Regarding the second assumption, it is critical that the property being optimized is physically well-defined on the domain of genomes represented in the fitness landscape. With these two assumptions satisfied, genetic algorithms are well-suited for the search for the genome that optimizes the fitness of a chosen set of materials.

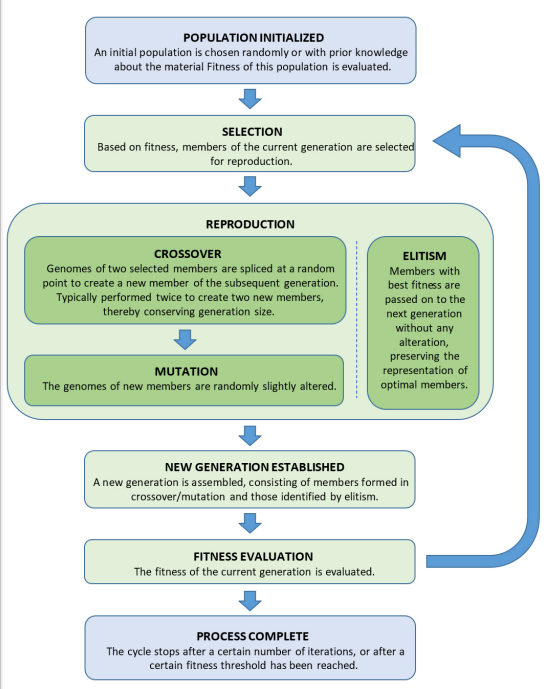
To determine the material with the optimal properties, evolutionary operations are applied to an initial population to produce subsequent generations of materials. Typically, the evolutionary operations employed are selection, reproduction, crossover, and mutation, though elitism may also be incorporated. The generic procedure of an evolutionary algorithm is shown in Figure 3. First, an initial population of materials is chosen. Often, the initial population is randomly selected, but it can incorporate prior knowledge about the material. For each generation, the fitness of each member is evaluated, and a selection of members is algorithmically chosen to create the next generation. As in natural selection, members with favorable properties receive preferential treatment; those with optimal fitness tend to be selected more frequently than their subpar counterparts. The selected members are then randomly paired for crossover: the genomes of the member pairs are randomly spliced together to create the genome for the member of the next generation. Subsequently, some members are subjected to mutation-their genome is slightly, randomly altered in at least one manner. In addition, some methods implement elitism. In this operation, a few of the top members are passed on to the next generation without any alteration, thus preserving some members that may be the optimal solution. These evolutionary operations are repeated for a certain number of generations or until a desired fitness is reached.

While the overarching purpose of a genetic algorithm is to determine the optimal material genome, evolutionary operations are dual-purpose. As previously discussed, the successful implementation of a genetic algorithm requires a thorough exploration of the fitness landscape, as learned through the fitness evaluation of a diverse population. Therefore, genetic algorithms require mechanisms for both genome optimization and exploration, conveniently provided by the assortment of evolutionary operations. The pseudo-deterministic aspect of the natural selection process, in which members with high fitness are given preference, inherently leads to an improvement of overall population fitness over the course of many generations. Conversely, the random aspects of the natural selection process, namely the probabilistic selection of members, as well as the intrinsic stochasticity in crossover and mutation, allow a broader examination of the fitness landscape. In this way, genetic algorithms integrate optimization with stochasticity to continually improve properties, without neglecting the exploration of parameter space.

Optimization of Inorganic Phosphors Using Genetic Algorithms

Considering Broad Applications of Genetic Algorithms in Materials Science

While not quite a common technique for materials scientists, genetic algorithms have found a wide variety of applications in the discipline.They have been used to identify low-energy configurations of elemental clusters for silicon, carbon, and silver, among others. They have been implemented for the design of alloys, nanowires, thin-films, ceramics, and more. They have played a significant role in the optimization of catalysts. These applications and more have been compiled and discussed in more than one prominent review article regarding genetic algorithms in materials science [1,10,20]. Therefore, the purpose of this work is not to repeat a list of research applications already detailed elsewhere. Rather, as previously noted, this work aims to detail the implementation of genetic algorithm approaches in a specific subfield: the discovery and optimization of inorganic phosphors. A thorough account of the use of genetic algorithms in this area serves two purposes. First, understanding the challenges faced in utilizing genetic algorithms in materials science elucidates their realm of applicability in the discipline, while also revealing how these approaches are uniquely suited to address certain problems. Second, and perhaps more importantly, the black box nature of these approaches raises questions regarding the role of machine learning in materials research and engineering, a discipline traditionally more receptive to rigorous basic research.

Early Methodology for Genetic Algorithm-Assisted Inorganic Phosphor Optimization

Due to developments in semiconductor technologies and advances in optics, light-emitting diodes (LEDs) have revolutionized lighting-with high intensity, efficiency, and affordability, white LEDs (WLEDs) are quickly replacing fluorescent and incandescent lighting. The increasing commercial application of WLEDs has created a need for long-lasting devices that can provide consistent, high-intensity light. As such, in the past decade, significant effort has been given to improving WLEDs. While there are several types of WLEDs, the optimal color rendition is provided by tricolor WLEDs, which use soft ultraviolet light to excite red, green, and blue (RGB) phosphors. To generate quality light, the chosen RGB phosphors must provide high luminescence efficiency and the ideal color balance. As such, the optimization of the luminescence of RGB phosphors is essential to further development of WLEDs.

In 2003, K.S. Sohn et al. applied an innovative approach to improving inorganic phosphors: genetic-algorithm assisted combinatorial chemistry (GACC), which combined genetic algorithm optimization with the experimental high-throughput synthesis of phosphors [24]. To begin, the group developed a solution-based, combinatorial chemistry method for the synthesis of a library of red phosphors. The inorganic oxide created was a Eu³⁺-activated alkali earth borosilicate system with varying amount of seven cations: Eu, Mg, Ca, Sr, Ba, B, and Si. The library featured 108 samples with a variety of compositions, chosen to reflect the existing knowledge about phosphors. After measuring emission and decay curves, the group calculated the luminance of each sample at 400 nm, the wavelength of an InGaN light source typically used in an LED. Based on the resulting data, the initial generation of samples was entered into the genetic algorithm. Each sample was identified in the genetic algorithm by the set of seven mole fractions, and the fitness of each sample was based on luminance.

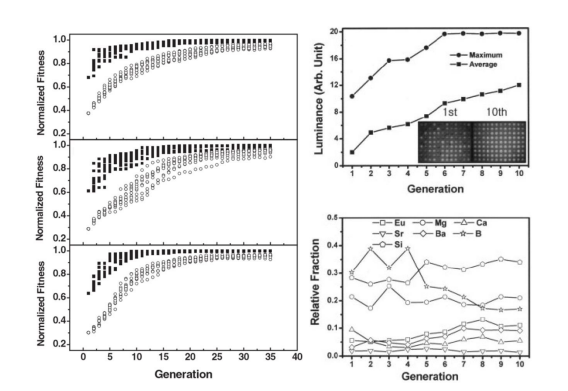
The objective of the genetic algorithm is, of course, to identify the composition of the sample with the maximum luminance, achieved through an evaluation of the fitness of each subsequent sample. However, the explicit relationship between material composition and luminance is obviously unknown; therefore, a hypothetical fitness function was chosen. In general, selecting a fitness function can be somewhat challenging; the function should ideally reflect the most significant trends in the data. To determine a suitable fitness function, Sohn et al. performed simulations of three different hypothetical functions and evaluated whether the choice of the fitness function would alter the optimization speed or the accuracy of the result. They found that all the fitness functions led to the same optimal point after ten generations, as shown in Figure 4a.

The genetic algorithm was then applied to the experimental data, and the optimization results are shown in Figure 4b. In the top panel, the maximum and average luminance are plotted as a function of generation. The luminance quickly improves with each generation and then converges after the sixth iteration. Moreover, the bottom panel shows the evolution of the composition as a function of generation. The material appears to be optimized by slightly tweaking most of the components while significantly decreasing the relative fraction of boron and essentially removing strontium. While these results are certainly promising, they are only useful if the material can be experimentally synthesized and if the resulting material does, in fact, show improvements in the luminance.

The inset in the top panel of Figure 4b provides experimental evidence of an improved set of materials. The first generation has population members with a wide range of luminesce while the tenth generation has members that are almost exclusively bright, demonstrating the success of GACC. The sample with the highest luminance was Eu_0.14Mg_0.18Ca_0.07Ba_0.12B_0.17 - Si_0.32O_δ , and other top members had similar compositions. The luminance of Eu_0.14Mg_0.18Ca_0.07Ba_0.12B_0.17 - Si_0.32O_δ was found to be five times higher than commercially available Y₂O₃ :Eu³⁺ and ten times higher than commercially available Y₂O₃ S:Eu³⁺ at 400 nm excitation. As could be expected, this material does not appear to be a stoichiometric single line compound, as verified by Joint Committee of Powder Diffraction Standards data and inorganic oxide phase diagrams. Rather, these members are most likely non-stoichiometric compounds with a variety of constituents and phases. From a materials science perspective, an in-depth investigation of the resulting material structure and properties is certainly desirable, and this topic is pursued by the author in a later publication. However, from a purely materials engineering perspective, the result within the scope of the project is self-evident: GACC was successfully utilized in the improvement of red inorganic phosphors, regardless of knowledge of the structure of the material or of the true relationship between material composition and luminance.

Criticism of Genetic Algorithm Approaches and the Development of Improved Methods

Over the next decade, this approach was used to optimize other groups of inorganic phosphors. Between 2005 and 2008, Sohn and his collaborators published similar works for the improvement of green [25], red [26,27], and blue [28] inorganic phosphors for a variety of systems. Unfortunately, few of these results led to commercial applications; only their work on Y(V,P)O₄ :Eu³⁺ phosphors was developed further in industry, for use in plasma display panels and liquid crystal display back light units. In fact, the results of these experiments were greatly overshadowed by more conventional research on phosphor materials during this time [29-32]. In a 2009 paper, A.K. Sharma identifies two main reasons for this: scalability and reproducibility [33]. Despite its high-throughput nature, the experimental method initially developed for these projects was found incompatible for mass-scale commercial production. Even more problematically, the synthesis procedure resulted in relatively high experimental inconsistencies, resulting in low reproducibility of the desired materials. In solid-state synthesis, this is considered somewhat inevitable; mixing behavior is typically somewhat unpredictable, leading to more variability in the results. These two glaring issues led to the GACC being criticized as “methodology for the methodology,” rather than a serious contributor to the development of commercial engineering materials. Despite these difficulties, proponents of genetic algorithm-assisted discovery and optimization of phosphors remained undeterred. Where some apparently viewed the research area as an inapplicable demonstration of methodology, researchers in the field considered these studies as preliminary research necessary in order to develop more refined and accurate mathematical models. At this point, it had become exceedingly evident that a simplistic single genetic algorithm would not be sufficient to address commercial-scale phosphor optimization; a greater degree of mathematical complexity was required. As such, research in the field made a significant shift from proof-of-concept demonstrations toward approaches with multiple evolutionary algorithm layers and an improved ability to handle complex optimizations.

In the same 2009 publication that identified the current limitations of GACC, Sharma et al. introduced a more refined approach for genetic algorithm-assisted optimization, specifically designed to address the reproducibility problem [33]. This method, multi-objective genetic algorithm-assisted combinatorial materials search (MOGACMS), provided methodology for the simultaneous maximization of luminance and minimization of an inconsistency index, resulting in the identification of inorganic phosphors that are both highly luminescent and consistent. To incorporate a measure of consistency, researchers regarded experimental inconsistency as a function of precursor solution composition, based on literature about solid-state synthesis. Comparing the luminance of two experimental libraries, the researchers defined the inconsistency index for each sample as the difference in luminance, and asserted that this was associated with the sample composition. MOGACMS, as detailed in previous studies, was then performed on an MnONa₂O-Li₂O-MgO-CaO-GeO₂ system, and an optimal phosphor was identified: Na²MgGeO₄ :Mn²⁺, referred to as NMG. NMG was found to be slightly less efficient than the established BAM phosphor, but to have improved chromaticity. Additionally, NMG was found to be slightly more efficient than the ZSM phosphor but with slightly inferior chromaticity, comparatively. Moreover, the phosphor was reliably reproduced, demonstrating the effectiveness of MOGACMS in identifying a suitable phosphor candidate. Due to its relatively impressive luminescence properties and its consistency, NMG demonstrates potential for commercial applications.

Addressing Industry Needs with Genetic Algorithm-Assisted Materials Discovery

As clearly demonstrated by the general criticism toward phosphor research lacking overt commercial potential, research in this area has been driven by industrial interests. Within the past five years, there has been another notable shift in the focus of inorganic phosphor research. With the surge in development of commercial WLEDs, many existing inorganic phosphor materials have been patented, necessitating the discovery of novel, structurally unique phosphors. As a result, research has shifted from the optimization of current phosphors to the identification of new materials, free of intellectual property complications. Of course, this switch of focus is somewhat ironic, considering the backlash toward genetic-algorithm assisted methods. Researchers were initially criticized for developing methodology that failed to prioritize the discovery and optimization of immediately commercially viable materials, yet intellectual property issues have inevitably necessitated the discovery of previously uninvestigated phosphors. Given this new concern, algorithm-assisted methods have become increasingly relevant: the ability to intelligently explore large parameter spaces is inarguably essential to the task of discovering innumerable new materials, and machine learning methods provide a cleanly structured procedure for doing so.

With phosphor research centered on novel phosphor discovery, algorithm-assisted methods shifted to more complex models capable of incorporating commercial needs for structurally unique materials. In 2012, W.B. Park et al. integrated a non-dominated-sorting genetic algorithm (NSGA) with a second evolutionary algorithm, particle swarm optimization (PSO), to discover new, inorganic phosphors from the SrO-CaO-BaO-La₂O₃ -Y₂O₃ -Si₃N₄ -Eu₂O₃ system [34]. NGSA and PSO were used consecutively to conduct a more structured search for an optimal phosphor; the NSGA broadly searched for promising regions in the parameter space, while PSO conducted a more refined search for an optimized phosphor within these regions. While this specific composition space contains several well-known phosphors, these phosphors were specifically excluded from the experimental search. As a result, the NSGA and PSO investigated solely novel materials.

Similar to MOGACMS, NSGAs are a type of multi- -objective genetic algorithm, capable of balancing the maximization or minimization of several parameters. The distinguishing characteristic of NSGAs is the method by which they manage multiple optimizations. Generally, a multi-objective optimization problem has two types of solutions: nondominated or dominated. A nondominated, or Pareto optimal, solution is an answer in which an objective cannot be improved except at the expense of other objectives. Conversely, a dominated solution is explicitly better than other solutions for all objectives. When a dominated solution is not present, several Pareto optimal solutions may exist and have equal validity. This set of optimized solutions is referred to as a Pareto front. The set of all possible solutions, including non-optimal ones, can be categorized in Pareto groups, which are sets of solutions that have equal validity within their group but may not offer the best optimization. More explicitly, the Pareto front is the Pareto group consisting of the set of equal (yet different) optimal solutions. NSGAs use Pareto groups to evaluate the potential optimal solutions to a problem.

In this study, the Pareto front consisted of solutions that simultaneously maximized photoluminescence (PL) intensity of the phosphor and minimized the “structural rank”. The structural rank was designed to reflect the novelty of the material, based on information from xray diffraction (XRD) databases; a low rank generally corresponded to an unknown phase while a high rank corresponded to a familiar XRD pattern or a damaged sample. To begin the genetic algorithm, an initial population was randomly chosen. As the genetic algorithm iterated through each generation, the PL intensity and structural rank were evaluated, and the samples were associated with Pareto groups. Relative fitness values were assigned to samples based on affiliation with Pareto groups, and the genetic algorithm proceeded. After four generations, the algorithm converged on a one-sample Pareto front, relegating all other samples to lesser Pareto groups. This optimal sample was centered on the CaO-La₂O₃ -Si₃N₄ -Eu₂O₃ quaternary composition.

Based on this result, PSO was implemented to explore the quaternary composition space. While an extensive discussion of PSO is outside of the scope of this work, details are readily available in the publication. PSO resulted in the identification of a novel phosphor with a promising PL intensity and spectral distribution, which demonstrates potential for WLEDs commercial applications: La₄ - _xCa_xSi₁₂O_3+xN_18-x:Eu²⁺ (x=1.456).

These results exemplify the utility of genetic algorithm-assisted methods for novel phosphor identification, demonstrated further by ensuing research in the field; equally successful results were achieved in similar studies by W.B. Park et al. in subsequent years [35-38]. Additionally, in 2019, R. Lv et al. implemented several computational techniques to identify the optimal activator concentration for a lanthanide phosphor to maximize the luminescent intensity. In comparing four techniques–PSO, another genetic algorithm approach, simulated annealing, and improved annealing with a harmony search algorithm–the study found that the genetic algorithm approach identified acceptable solutions at lower experimental time and cost, relative to the other approaches. Further, PSO identified the highest luminescent intensity given the most generations [39]. This growing body of studies suggests that genetic algorithms and PSO can provide value in the identification of novel inorganic phosphors.

Moving Forward: Expanding Data Sources for the Identification of Novel Inorganic Phosphors and Other Inorganic Functional Materials

While researchers have successfully used genetic algorithms and PSO to identify novel inorganic phosphors with desirable characteristics, the availability and growth of materials databases present new opportunities for improving techniques in the future. In a 2018 study, J. Brgoch et al. established a new approach for phosphor screening methods by merging supervised machine learning to predict Debye temperature with high-throughput calculations using DFT to approximate band gap. The authors determined the Debye temperature for 2,610 DFT-based moduli from the Materials Project database and employed the results to train their model for determining Debye temperature. After establishing the training set, the authors could apply the model to estimate Debye temperatures of compounds compiled in crystallographic databases, and particularly selected compounds with available information on bandgap, among other criteria. Ultimately, the authors used this method to identify one specific inorganic phosphor crystal structure that stood out among 2071 materials [40].

Though this study utilized a different form of machine learning–support vector machine regression–it is notable in the context of this work, as it exemplifies the opportunity to employ big data from materials databases into the identification of novel inorganic phosphors. As explained in the paper by C. Park et al.: “Brgoch et al. sorted out the data paucity problem by employing a massive amount of DFT-generated data for inorganic compounds (including non-phosphor materials) residing in a well-established database as training data and further expanding the fully trained [machine learning] model to a small phosphor dataset. This could be considered a brilliant case of transfer learning, which currently is a booming trend in applications of [machine learning].” [41].

Future work in the identification of novel inorganic phosphors could benefit from more extensive investigation and integration of data from various materials databases, including DFT data as well as XRD data, as investigated by B.D. Lee et al. [42].

Summary, Concluding Observations, and Future Research Directions

Despite their relatively gradual entrance into the realm of materials science and engineering, genetic algorithms and other forms of machine learning have made noteworthy contributions in a broad range of subfields; yet, more significantly, these algorithms demonstrate the potential to address certain research topics in ways other methods cannot. The need for novel and distinct commercial materials is continually growing, and evolutionary algorithms are especially suited to combinatorial exploration and optimization. This was particularly evident in the case of the discovery of inorganic phosphors; while machine learning methods initially fell short of conventional methods, the industrial demand for high-throughput materials discovery inevitably led to the triumph of genetic algorithm-assisted methods. This case study exemplifies the strength of genetic algorithm-based methods: solving highly applied problems in materials engineering. These methods individually are not ideal for developing a fundamental understanding of an underlying mechanism, a goal frequently sought in basic materials research-with a black box approach, evolutionary algorithms allow researchers to perform optimization, not understand the basic science leading to the optimization.

While evolutionary algorithms and other forms of machine learning may not provide insight into the fundamental mechanisms underlying materials properties, they are progressively becoming viable methods for the improvement of commercial materials. As such, the demand for new and improved materials could result in the increasing application of algorithm-assisted optimization approaches, particularly by materials scientists and engineers in industry. Additional work remains, however, to mitigate the challenges of implementing these computational methods. To address concerns about interpretability of machine learning models and results, future research is needed to refine approaches for pairing machine learning techniques with first-principles computational methodologies, to reap the benefits of machine learning assisted optimization while meeting expectations for conducting basic scientific research. Further, the use of machine learning in materials science continues to be limited by available data that can inform models. Initiatives such as the MGI support the development of robust datasets and tools that enable researchers to integrate machine learning techniques into their work. These datasets and tools, however, are still being built. Enhanced efforts to improve the findability, accessibility, interoperability, and reusability of materials data, such as through the implementation of “FAIR Guiding Principles for Scientific Data Management and Stewardship” could improve opportunities for materials science researchers to leverage machine learning techniques [43].